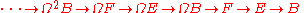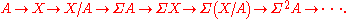Eckmann–Hilton duality
Encyclopedia
In the mathematical disciplines of algebraic topology
and homotopy theory, Eckmann–Hilton duality in its most basic form, consists of taking a given diagram
for a particular concept and reversing the direction of all arrows, much as in category theory
with the idea of the opposite category
.
It is named after Beno Eckmann
and Peter Hilton
.
For example, the fact that the dual notion of a limit
is a colimit allows us to change the Eilenberg–Steenrod axioms for homology to give axioms for cohomology.
Another example is given by currying
, which tells us that for any object , a map
, a map 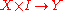 is the same as a map
is the same as a map  , where
, where 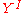 is the exponential object
is the exponential object
, given by all maps from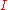 to
to  . In the case of topological spaces, if we take
. In the case of topological spaces, if we take  to be the unit interval, this leads to a duality between
to be the unit interval, this leads to a duality between  and
and 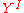 which then gives a duality between
which then gives a duality between
the reduced suspension which is a quotient of
which is a quotient of  and
and
the loop space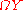 which is a subspace of
which is a subspace of  .
.
This then leads to the adjoint relation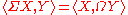 which allows the study of spectra
which allows the study of spectra
which give rise to cohomology theories
.
We can also directly relate fibration
s and cofibration
s: a fibration is defined by having the homotopy lifting property
is defined by having the homotopy lifting property
, represented by the following diagram
 and a cofibration
and a cofibration  is defined by having the dual homotopy extension property
is defined by having the dual homotopy extension property
, represented by dualising the previous diagram:
 The above considerations also apply when looking at the sequences associated to a fibration or a cofibration, as given a fibration
The above considerations also apply when looking at the sequences associated to a fibration or a cofibration, as given a fibration  we get the sequence
we get the sequence
and given a cofibration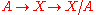 we get the sequence
we get the sequence
This also allows us to relate homotopy and cohomology: we know that homotopy groups are homotopy classes of maps from the n-sphere to our space, written , and we know that the sphere has a single nonzero (reduced) cohomology group. On the other hand, cohomology groups are homotopy classes of maps to spaces with a single nonzero homotopy group. This is given by the Eilenberg–MacLane spaces
, and we know that the sphere has a single nonzero (reduced) cohomology group. On the other hand, cohomology groups are homotopy classes of maps to spaces with a single nonzero homotopy group. This is given by the Eilenberg–MacLane spaces 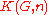 and the relation
and the relation 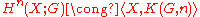 .
.
Algebraic topology
Algebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...
and homotopy theory, Eckmann–Hilton duality in its most basic form, consists of taking a given diagram
Diagram (category theory)
In category theory, a branch of mathematics, a diagram is the categorical analogue of an indexed family in set theory. The primary difference is that in the categorical setting one has morphisms. An indexed family of sets is a collection of sets, indexed by a fixed set; equivalently, a function...
for a particular concept and reversing the direction of all arrows, much as in category theory
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
with the idea of the opposite category
Opposite category
In category theory, a branch of mathematics, the opposite category or dual category Cop of a given category C is formed by reversing the morphisms, i.e. interchanging the source and target of each morphism. Doing the reversal twice yields the original category, so the opposite of an opposite...
.
It is named after Beno Eckmann
Beno Eckmann
Beno Eckmann was a Swiss mathematician who was a student of Heinz Hopf.Born in Bern, Eckmann received his master's degree from Eidgenössische Technische Hochschule Zürich in 1931. Later he studied there under Heinz Hopf, obtaining his Ph.D. in 1941...
and Peter Hilton
Peter Hilton
Peter John Hilton was a British mathematician, noted for his contributions to homotopy theory and for code-breaking during the Second World War.-Life:Hilton was born in London, and educated at St Paul's School...
.
For example, the fact that the dual notion of a limit
Limit (category theory)
In category theory, a branch of mathematics, the abstract notion of a limit captures the essential properties of universal constructions such as products and inverse limits....
is a colimit allows us to change the Eilenberg–Steenrod axioms for homology to give axioms for cohomology.
Another example is given by currying
Currying
In mathematics and computer science, currying is the technique of transforming a function that takes multiple arguments in such a way that it can be called as a chain of functions each with a single argument...
, which tells us that for any object
 , a map
, a map 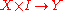 is the same as a map
is the same as a map  , where
, where 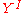 is the exponential object
is the exponential objectExponential object
In mathematics, specifically in category theory, an exponential object is the categorical equivalent of a function space in set theory. Categories with all finite products and exponential objects are called cartesian closed categories...
, given by all maps from
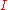 to
to  . In the case of topological spaces, if we take
. In the case of topological spaces, if we take  to be the unit interval, this leads to a duality between
to be the unit interval, this leads to a duality between  and
and 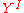 which then gives a duality between
which then gives a duality betweenthe reduced suspension
 which is a quotient of
which is a quotient of  and
andthe loop space
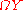 which is a subspace of
which is a subspace of  .
.This then leads to the adjoint relation
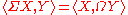 which allows the study of spectra
which allows the study of spectraSpectrum (homotopy theory)
In algebraic topology, a branch of mathematics, a spectrum is an object representing a generalized cohomology theory. There are several different constructions of categories of spectra, any of which gives a context for the same stable homotopy theory....
which give rise to cohomology theories
Cohomology
In mathematics, specifically in algebraic topology, cohomology is a general term for a sequence of abelian groups defined from a co-chain complex. That is, cohomology is defined as the abstract study of cochains, cocycles, and coboundaries...
.
We can also directly relate fibration
Fibration
In topology, a branch of mathematics, a fibration is a generalization of the notion of a fiber bundle. A fiber bundle makes precise the idea of one topological space being "parameterized" by another topological space . A fibration is like a fiber bundle, except that the fibers need not be the same...
s and cofibration
Cofibration
In mathematics, in particular homotopy theory, a continuous mappingi\colon A \to X,where A and X are topological spaces, is a cofibration if it satisfies the homotopy extension property with respect to all spaces Y. The name is because the dual condition, the homotopy lifting property, defines...
s: a fibration
 is defined by having the homotopy lifting property
is defined by having the homotopy lifting propertyHomotopy lifting property
In mathematics, in particular in homotopy theory within algebraic topology, the homotopy lifting property is a technical condition on a continuous function from a topological space E to another one, B...
, represented by the following diagram

 is defined by having the dual homotopy extension property
is defined by having the dual homotopy extension propertyHomotopy extension property
In mathematics, in the area of algebraic topology, the homotopy extension property indicates when a homotopy defined on a subspace can be extended to a homotopy defined on a larger space.-Definition:Let X\,\! be a topological space, and let A \subset X....
, represented by dualising the previous diagram:

 we get the sequence
we get the sequenceand given a cofibration
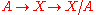 we get the sequence
we get the sequenceThis also allows us to relate homotopy and cohomology: we know that homotopy groups are homotopy classes of maps from the n-sphere to our space, written
 , and we know that the sphere has a single nonzero (reduced) cohomology group. On the other hand, cohomology groups are homotopy classes of maps to spaces with a single nonzero homotopy group. This is given by the Eilenberg–MacLane spaces
, and we know that the sphere has a single nonzero (reduced) cohomology group. On the other hand, cohomology groups are homotopy classes of maps to spaces with a single nonzero homotopy group. This is given by the Eilenberg–MacLane spaces 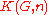 and the relation
and the relation 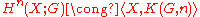 .
.