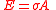Dynamic fluid film equations
Encyclopedia
Fluid films, such as soap film
s, are commonly encountered in everyday experience. A soap film can be formed by dipping a closed contour wire into a soapy solution as in the figure on the right. Alternatively, a catenoid
can be formed by dipping two rings in the soapy solution and subsequently separating them while maintaining the coaxial configuration.
Stationary fluid films form surfaces of minimal surface area
, leading to the Plateau problem.
On the other hand, fluid films display fascinating and rich dynamic properties. They can undergo enormous deformations away from the equilibrium configuration. Furthermore, they display several orders of magnitude variations in thickness from nanometers to millimeters. Thus, a fluid film can simultaneously display nanoscale and macroscale phenomena.
In the study of the dynamics
of free fluid films, such as soap film
s, it is common to model the film as two dimensional manifolds. Then the variable thickness of the film is captured by the two dimensional density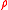 .
.
The dynamics of fluid films can be described by the following system of exact nonlinear Hamiltonian equations
which, in that respect, are a complete analogue of Euler's inviscid equations of fluid dynamics
. In fact, these equations reduce to Euler's dynamic equations for flows in stationary Euclidean spaces.
The forgoing relies on the formalism of tensors, including the summation convention and the raising and lowering of tensor indices
.
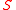 that spans a stationary closed contour boundary. Let
that spans a stationary closed contour boundary. Let  be the normal component of the velocity field and
be the normal component of the velocity field and 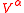 be the contravariant components of the tangential velocity projection. Let
be the contravariant components of the tangential velocity projection. Let 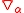 be the covariant surface derivative,
be the covariant surface derivative,  be the covariant curvature tensor
be the covariant curvature tensor
,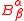 be the mixed curvature tensor
be the mixed curvature tensor
and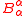 be its trace
be its trace
, that is mean curvature
. Furthermore, let the internal energy
density per unit mass function be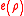 so that the total potential energy
so that the total potential energy
 is given by
is given by
This choice of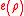 :
:
where is the surface energy density results in Laplace's classical model for surface tension
is the surface energy density results in Laplace's classical model for surface tension
:
where A is the total area of the soap film.
The governing system reads
Soap film
Soap films are thin layers of liquid surrounded by air. For example, if two soap bubbles enters in contact, they merged and a thin film is created in between. Thus, foams are composed of a network of films connected by Plateau borders...
s, are commonly encountered in everyday experience. A soap film can be formed by dipping a closed contour wire into a soapy solution as in the figure on the right. Alternatively, a catenoid
Catenoid
A catenoid is a three-dimensional surface made by rotating a catenary curve about its directrix. Not counting the plane, it is the first minimal surface to be discovered. It was found and proved to be minimal by Leonhard Euler in 1744. Early work on the subject was published also by Jean Baptiste...
can be formed by dipping two rings in the soapy solution and subsequently separating them while maintaining the coaxial configuration.
Stationary fluid films form surfaces of minimal surface area
Minimal surface
In mathematics, a minimal surface is a surface with a mean curvature of zero.These include, but are not limited to, surfaces of minimum area subject to various constraints....
, leading to the Plateau problem.
On the other hand, fluid films display fascinating and rich dynamic properties. They can undergo enormous deformations away from the equilibrium configuration. Furthermore, they display several orders of magnitude variations in thickness from nanometers to millimeters. Thus, a fluid film can simultaneously display nanoscale and macroscale phenomena.
In the study of the dynamics
Dynamics
Dynamics may refer to:-Physics and engineering:* Dynamics , the time evolution of physical processes** Aerodynamics, the study of gases in motion...
of free fluid films, such as soap film
Soap film
Soap films are thin layers of liquid surrounded by air. For example, if two soap bubbles enters in contact, they merged and a thin film is created in between. Thus, foams are composed of a network of films connected by Plateau borders...
s, it is common to model the film as two dimensional manifolds. Then the variable thickness of the film is captured by the two dimensional density
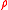 .
.The dynamics of fluid films can be described by the following system of exact nonlinear Hamiltonian equations
Hamiltonian system
In physics and classical mechanics, a Hamiltonian system is a physical system in which forces are momentum invariant. Hamiltonian systems are studied in Hamiltonian mechanics....
which, in that respect, are a complete analogue of Euler's inviscid equations of fluid dynamics
Fluid dynamics
In physics, fluid dynamics is a sub-discipline of fluid mechanics that deals with fluid flow—the natural science of fluids in motion. It has several subdisciplines itself, including aerodynamics and hydrodynamics...
. In fact, these equations reduce to Euler's dynamic equations for flows in stationary Euclidean spaces.
The forgoing relies on the formalism of tensors, including the summation convention and the raising and lowering of tensor indices
Raising and lowering indices
In mathematics and mathematical physics, given a tensor on a manifold M, in the presence of a nonsingular form on M , one can raise or lower indices: change a type tensor to a tensor or to a tensor...
.
The full dynamic system
Consider a thin fluid film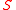 that spans a stationary closed contour boundary. Let
that spans a stationary closed contour boundary. Let  be the normal component of the velocity field and
be the normal component of the velocity field and 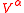 be the contravariant components of the tangential velocity projection. Let
be the contravariant components of the tangential velocity projection. Let 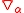 be the covariant surface derivative,
be the covariant surface derivative,  be the covariant curvature tensor
be the covariant curvature tensorCurvature tensor
In differential geometry, the term curvature tensor may refer to:* the Riemann curvature tensor of a Riemannian manifold — see also Curvature of Riemannian manifolds;* the curvature of an affine connection or covariant derivative ;...
,
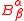 be the mixed curvature tensor
be the mixed curvature tensorCurvature tensor
In differential geometry, the term curvature tensor may refer to:* the Riemann curvature tensor of a Riemannian manifold — see also Curvature of Riemannian manifolds;* the curvature of an affine connection or covariant derivative ;...
and
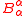 be its trace
be its traceTrace (linear algebra)
In linear algebra, the trace of an n-by-n square matrix A is defined to be the sum of the elements on the main diagonal of A, i.e.,...
, that is mean curvature
Mean curvature
In mathematics, the mean curvature H of a surface S is an extrinsic measure of curvature that comes from differential geometry and that locally describes the curvature of an embedded surface in some ambient space such as Euclidean space....
. Furthermore, let the internal energy
Internal energy
In thermodynamics, the internal energy is the total energy contained by a thermodynamic system. It is the energy needed to create the system, but excludes the energy to displace the system's surroundings, any energy associated with a move as a whole, or due to external force fields. Internal...
density per unit mass function be
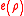 so that the total potential energy
so that the total potential energyPotential energy
In physics, potential energy is the energy stored in a body or in a system due to its position in a force field or due to its configuration. The SI unit of measure for energy and work is the Joule...
 is given by
is given byThis choice of
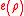 :
:where
 is the surface energy density results in Laplace's classical model for surface tension
is the surface energy density results in Laplace's classical model for surface tensionSurface tension
Surface tension is a property of the surface of a liquid that allows it to resist an external force. It is revealed, for example, in floating of some objects on the surface of water, even though they are denser than water, and in the ability of some insects to run on the water surface...
:
where A is the total area of the soap film.
The governing system reads
-
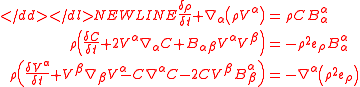
where the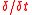 -derivative is the central operator, originally
-derivative is the central operator, originally
due to Jacques HadamardJacques HadamardJacques Salomon Hadamard FRS was a French mathematician who made major contributions in number theory, complex function theory, differential geometry and partial differential equations.-Biography:...
, in the The Calculus of Moving Surfaces. Note that, in compressible models, the combination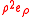 is commonly
is commonly
identified with pressure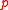 . The governing system above was originally formulated in reference 1.
. The governing system above was originally formulated in reference 1.
For the Laplace choice of surface tension the system becomes:
the system becomes:
-

Note that on flat (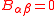 ) stationary (
) stationary ( ) manifolds, the
) manifolds, the
system becomes
-
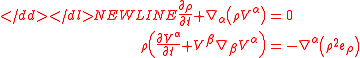
which is precisely classical Euler's equations of fluid dynamics.
A simplified system
If one disregards the tangential components of the velocity field, as frequently done in the study of thin fluid film, one arrives at the following simplified system with only two unknowns: the two dimensional density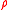 and the normal velocity
and the normal velocity  :
:
-
-
-