
Dual basis in a field extension
Encyclopedia
In mathematics
, the linear algebra
concept of dual basis can be applied in the context of a finite extension L/K, by using the field trace
. This requires the property that the field trace TrL/K provides a non-degenerate quadratic form
over K. This can be guaranteed if the extension is separable
; it is automatically true if K is a perfect field
, and hence in the cases where K is finite, or of characteristic zero.
A dual basis isn't a concrete basis
like the polynomial basis
or the normal basis
; rather it provides a way of using a second basis for computations.
Consider two bases for elements in a finite field
, GF(pm):
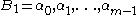
and
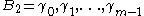
then B2 can be considered a dual basis of B1 provided
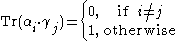
Here the trace
of a value in GF(pm) can be calculated as follows:
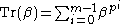
Using a dual basis can provide a way to easily communicate between devices that use different bases, rather than having to explicitly convert between bases using the change of bases formula. Furthermore, if a dual basis is implemented then conversion from an element in the original basis to the dual basis can be accomplished with a multiplication by the multiplicative identity (usually 1).
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the linear algebra
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
concept of dual basis can be applied in the context of a finite extension L/K, by using the field trace
Field trace
In mathematics, the field trace is a function defined with respect to a finite field extension L/K. It is a K-linear map from L to K...
. This requires the property that the field trace TrL/K provides a non-degenerate quadratic form
Quadratic form
In mathematics, a quadratic form is a homogeneous polynomial of degree two in a number of variables. For example,4x^2 + 2xy - 3y^2\,\!is a quadratic form in the variables x and y....
over K. This can be guaranteed if the extension is separable
Separable extension
In modern algebra, an algebraic field extension E\supseteq F is a separable extension if and only if for every \alpha\in E, the minimal polynomial of \alpha over F is a separable polynomial . Otherwise, the extension is called inseparable...
; it is automatically true if K is a perfect field
Perfect field
In algebra, a field k is said to be perfect if any one of the following equivalent conditions holds:* Every irreducible polynomial over k has distinct roots.* Every polynomial over k is separable.* Every finite extension of k is separable...
, and hence in the cases where K is finite, or of characteristic zero.
A dual basis isn't a concrete basis
Basis (linear algebra)
In linear algebra, a basis is a set of linearly independent vectors that, in a linear combination, can represent every vector in a given vector space or free module, or, more simply put, which define a "coordinate system"...
like the polynomial basis
Polynomial basis
In mathematics, the polynomial basis is a basis for finite extensions of finite fields.Let α ∈ GF be the root of a primitive polynomial of degree m over GF...
or the normal basis
Normal basis
In mathematics, a normal basis in field theory is a special kind of basis for Galois extensions of finite degree, characterised as forming a single orbit for the Galois group. The normal basis theorem states that any finite Galois extension of fields has a normal basis...
; rather it provides a way of using a second basis for computations.
Consider two bases for elements in a finite field
Finite field
In abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
, GF(pm):
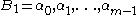
and
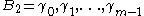
then B2 can be considered a dual basis of B1 provided
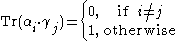
Here the trace
Field trace
In mathematics, the field trace is a function defined with respect to a finite field extension L/K. It is a K-linear map from L to K...
of a value in GF(pm) can be calculated as follows:
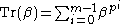
Using a dual basis can provide a way to easily communicate between devices that use different bases, rather than having to explicitly convert between bases using the change of bases formula. Furthermore, if a dual basis is implemented then conversion from an element in the original basis to the dual basis can be accomplished with a multiplication by the multiplicative identity (usually 1).

