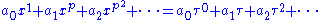Drinfel'd module
Encyclopedia
In mathematics
, a Drinfel'd module (or elliptic module) is roughly a special kind of module
over a ring of functions on a curve over a finite field
, generalizing the Carlitz module. Loosely speaking, they provide a function field analogue of complex multiplication
theory. A shtuka (also called F-sheaf or chtouca) is a sort of generalization of a Drinfel'd module, consisting roughly of a vector bundle
over a curve, together with some extra structure identifying a "Frobenius twist" of the bundle with a "modification" of it.
Drinfel'd modules were introduced by , who used them to prove the Langlands conjectures for GL2 of a function field
in some special cases. He later invented shtukas and used shtukas of rank 2 to prove
the remaining cases of the Langlands conjectures for GL2. Laurent Lafforgue
proved the Langlands conjectures for GLn of a function field by studying the moduli stack of shtukas of rank n.
"Shtuka" is a Russian word штука meaning "a single copy", which comes from the German noun “Stück” meaning “piece, item, or unit", and is unrelated to the German word Stuka, meaning dive bomber.
for a∈ L. The element τ can be thought of as a Frobenius element: in fact, L is a left module over L{τ}, with elements of L acting as multiplication and τ acting as the Frobenius endomorphism of L. The ring L{τ} can also be thought of as the ring of all (absolutely) additive polynomials
in L[x],
where a polynomial f is called additive
if f(x + y) = f(x) + f(y) (as elements of L[x,y]). The ring of additive polynomials is generated as an algebra over L by the polynomial τ = xp. The multiplication in the ring of additive polynomials is given by composition of polynomials, not by multiplication of commutative polynomials, and is not commutative.
a Drinfel'd A-module over L is defined to be a ring homomorphism ψ from A to
L{τ}, such that the image is not contained in L.
The ring A will usually be a ring of functions on some affine curve over a finite field.
The condition that the image of A is not in L is a non-degeneracy condition, put in to eliminate trivial cases.
As L{τ} can be thought of as endomorphisms of the additive group of L, a Drinfel'd A-module can be regarded as an action of A on the additive group of L, or in other words as an A-module whose underlying additive group is the additive group of L.
A (right) shtuka of rank r over a scheme
(or stack) U is given by the following data:
whose cokernels are supported on certain graphs of morphisms from U to X (called the zero and pole of the shtuka, and usually denoted by 0 and ∞), and are locally free of rank 1 on their supports. Here (Fr×1)*E is the pullback of E by the Frobenious endomorphism of U.
A left shtuka is defined in the same way except that the direction of the morphisms is reversed. If the pole and zero of the shtuka are disjoint then left shtukas and right shtukas are essentially the same.
By varying U, we get an algebraic stack Shtukar of shtukas of rank r, a "universal" shtuka over Shtukar×X and a morphism (∞,0) from Shtukar to X×X which is smooth and of relative dimension 2r−2. The stack Shtukar is not of finite type for r>1.
Drinfel'd modules are in some sense special kinds of shtukas. (This is not at all obvious from the definitions.) More precisely, Drinfel'd showed how to construct a shtuka from a Drinfel'd module.
See Drinfel'd, V. G. Commutative subrings of certain noncommutative rings. Funkcional. Anal. i Prilovzen. 11 (1977), no. 1, 11–14, 96. for details.
The "hard" part of proving these conjectures is to construct Galois representations with certain properties, and Drinfel'd constructed the necessary Galois representations by finding them inside the l-adic cohomology of certain moduli spaces of rank 2 shtukas.
Drinfel'd suggested that moduli spaces of shtukas of rank r could be used in a similar way to prove the Langlands conjectures for GLr; the formidable technical problems involved in carrying out this program were solved by Lafforgue after many years of effort.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a Drinfel'd module (or elliptic module) is roughly a special kind of module
Module (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
over a ring of functions on a curve over a finite field
Finite field
In abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
, generalizing the Carlitz module. Loosely speaking, they provide a function field analogue of complex multiplication
Complex multiplication
In mathematics, complex multiplication is the theory of elliptic curves E that have an endomorphism ring larger than the integers; and also the theory in higher dimensions of abelian varieties A having enough endomorphisms in a certain precise sense In mathematics, complex multiplication is the...
theory. A shtuka (also called F-sheaf or chtouca) is a sort of generalization of a Drinfel'd module, consisting roughly of a vector bundle
Vector bundle
In mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X : to every point x of the space X we associate a vector space V in such a way that these vector spaces fit together...
over a curve, together with some extra structure identifying a "Frobenius twist" of the bundle with a "modification" of it.
Drinfel'd modules were introduced by , who used them to prove the Langlands conjectures for GL2 of a function field
Function field of an algebraic variety
In algebraic geometry, the function field of an algebraic variety V consists of objects which are interpreted as rational functions on V...
in some special cases. He later invented shtukas and used shtukas of rank 2 to prove
the remaining cases of the Langlands conjectures for GL2. Laurent Lafforgue
Laurent Lafforgue
Laurent Lafforgue is a French mathematician.He won 2 silver medals at International Mathematical Olympiad in 1984 and 1985....
proved the Langlands conjectures for GLn of a function field by studying the moduli stack of shtukas of rank n.
"Shtuka" is a Russian word штука meaning "a single copy", which comes from the German noun “Stück” meaning “piece, item, or unit", and is unrelated to the German word Stuka, meaning dive bomber.
The ring of additive polynomials
We let L be a field of characteristic p>0. The ring L{τ} is defined to be the ring of noncommutative (or twisted) polynomials a0 + a1τ + a2τ2 + ... over L, with the multiplication given by- τa = apτ
for a∈ L. The element τ can be thought of as a Frobenius element: in fact, L is a left module over L{τ}, with elements of L acting as multiplication and τ acting as the Frobenius endomorphism of L. The ring L{τ} can also be thought of as the ring of all (absolutely) additive polynomials
in L[x],
where a polynomial f is called additive
Additive polynomial
In mathematics, the additive polynomials are an important topic in classical algebraic number theory.-Definition:Let k be a field of characteristic p, with p a prime number. A polynomial P with coefficients in k is called an additive polynomial, or a Frobenius polynomial, ifP=P+P\,as polynomials...
if f(x + y) = f(x) + f(y) (as elements of L[x,y]). The ring of additive polynomials is generated as an algebra over L by the polynomial τ = xp. The multiplication in the ring of additive polynomials is given by composition of polynomials, not by multiplication of commutative polynomials, and is not commutative.
Definition of Drinfel'd modules
If A is a commutative ring, thena Drinfel'd A-module over L is defined to be a ring homomorphism ψ from A to
L{τ}, such that the image is not contained in L.
The ring A will usually be a ring of functions on some affine curve over a finite field.
The condition that the image of A is not in L is a non-degeneracy condition, put in to eliminate trivial cases.
As L{τ} can be thought of as endomorphisms of the additive group of L, a Drinfel'd A-module can be regarded as an action of A on the additive group of L, or in other words as an A-module whose underlying additive group is the additive group of L.
Examples of Drinfel'd modules
- Define A to be Fp[T], the usual (commutative!) ring of polynomials over the finite fieldFinite fieldIn abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
of order p. In other words A is the coordinate ring of an affine genus 0 curve. Then a Drinfel'd module ψ is determined by the image ψ(T) of T, which can be any non-constant element of L{τ}. So Drinfel'd modules can be identified with non-constant elements of L{τ}. (In the higher genus case the description of Drinfel'd modules is more complicated.)
- The Carlitz module is the Drinfel'd module ψ given by ψ(T) = T+τ, where A is Fp[T] and L is a suitable complete algebraically closed field containing A. It was described by L. CarlitzLeonard CarlitzLeonard Carlitz was an American mathematician. Carlitz supervised 44 Doctorates at Duke University and published over 770 papers.- Chronology :* 1907 Born Philadelphia, PA, USA* 1927 BA, University of Pennsylvania...
in 1935, many years before the general definition of Drinfel'd module. See chapter 3 of Goss's book for more information about the Carlitz module.
Shtukas
Suppose that X is a curve over the finite field Fp.A (right) shtuka of rank r over a scheme
Scheme (mathematics)
In mathematics, a scheme is an important concept connecting the fields of algebraic geometry, commutative algebra and number theory. Schemes were introduced by Alexander Grothendieck so as to broaden the notion of algebraic variety; some consider schemes to be the basic object of study of modern...
(or stack) U is given by the following data:
- Locally free sheaves E, E′ of rank r over U×X together with injective morphisms
- E → E′ ← (Fr×1)*E,
whose cokernels are supported on certain graphs of morphisms from U to X (called the zero and pole of the shtuka, and usually denoted by 0 and ∞), and are locally free of rank 1 on their supports. Here (Fr×1)*E is the pullback of E by the Frobenious endomorphism of U.
A left shtuka is defined in the same way except that the direction of the morphisms is reversed. If the pole and zero of the shtuka are disjoint then left shtukas and right shtukas are essentially the same.
By varying U, we get an algebraic stack Shtukar of shtukas of rank r, a "universal" shtuka over Shtukar×X and a morphism (∞,0) from Shtukar to X×X which is smooth and of relative dimension 2r−2. The stack Shtukar is not of finite type for r>1.
Drinfel'd modules are in some sense special kinds of shtukas. (This is not at all obvious from the definitions.) More precisely, Drinfel'd showed how to construct a shtuka from a Drinfel'd module.
See Drinfel'd, V. G. Commutative subrings of certain noncommutative rings. Funkcional. Anal. i Prilovzen. 11 (1977), no. 1, 11–14, 96. for details.
Applications
The Langlands conjectures for functions fields state (very roughly) that there is a bijection between cuspidal automorphic representations of GLn and certain representations of a Galois group. Drinfel'd used Drinfel'd modules to prove some special cases of the Langlands conjectures, and later proved the full Langlands conjectures for GL2 by generalizing Drinfel'd modules to shtukas.The "hard" part of proving these conjectures is to construct Galois representations with certain properties, and Drinfel'd constructed the necessary Galois representations by finding them inside the l-adic cohomology of certain moduli spaces of rank 2 shtukas.
Drinfel'd suggested that moduli spaces of shtukas of rank r could be used in a similar way to prove the Langlands conjectures for GLr; the formidable technical problems involved in carrying out this program were solved by Lafforgue after many years of effort.
Shtukas
- Drinfel'd, V. G. Cohomology of compactified moduli varieties of F-sheaves of rank 2. (Russian) Zap. Nauchn. Sem. Leningrad. Otdel. Mat. Inst. Steklov. (LOMILomiLomi or Pancit Lomi is a Filipino-Chinese dish made with a variety of thick fresh egg noodles of about a quarter of an inch in diameter. Because of its popularity at least in the eastern part of Batangas, there are as many styles of cooking lomi as there are eateries, panciterias or restaurants...
) 162 (1987), Avtomorfn. Funkts. i Teor. Chisel. III, 107—158, 189; translation in J. Soviet Math. 46 (1989), no. 2, 1789–1821 - Drinfel'd, V. G. Moduli varieties of F-sheaves. (Russian) Funktsional. Anal. i Prilozhen. 21 (1987), no. 2, 23—41. English translation: Functional Anal. Appl. 21 (1987), no. 2, 107-122.
- D. Goss, What is a shtuka? Notices of the Amer. Math. Soc. Vol. 50 No. 1 (2003)