
Drainage equation
Encyclopedia
A drainage equation is an equation describing the relation between depth and spacing of parallel subsurface drains
, depth of the watertable, depth and hydraulic conductivity
of the soils. It is used in drainage
design.
A well known steady-state drainage equation is the Hooghoudt drain spacing equation. Its original publication is in Dutch. The equation was introduced in the USA by van Schilfgaarde.
where:
Steady (equilibrium) state condition
In steady state
, the level of the water table remains constant and the discharge rate (Q) equals the rate of groundwater recharge (R), i.e. the amount of water entering the groundwater
through the watertable per unit of time. By considering a long-term (e.g. seasonal) average depth of the water table (Dw) in combination with the long-term average recharge rate (R), the net storage of water in that period of time is negligibly small and the steady state condition is satisfied: one obtains a dynamic equilibrium
.
Derivation of the equation
For the derivation of the equation Hooghoudt used the law of Darcy
, the summation of circular potential functions
and, for the determination of the influence of the impermeable layer, de method of mirror image
s and superposition
.
Hooghoudt published tables for the determination of the equivalent depth (d), because the function (F) in d = F (L,Di-Dd,r) consists of long series of terms.
 Determining:
Determining:
the design drain spacing (L) can be found from the equation in dependence of the drain depth (Dd) and drain radius (r).
Drainage criteria
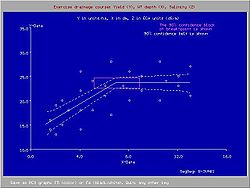
One would not want the water table to be too shallow to avoid crop yield depression nor too deep to avoid drought conditions. This is a subject of drainage research
. The figure shows that a seasonal average depth of the water table shallower than 70 cm causes a yield depression
The figure was made with the SegReg program for segmented regression
.
was developed for the equivalent depth (d) that can replace the Hooghoudt tables :
where:
in electricity.
It is in the form of a differential equation
that cannot be solved analytically (i.e. in a closed form
) but the solution requires a numerical method for which a computer program
is indispensable.
The availability of a computer program also helps in quickly assessing various alternatives and performing a sensitivity analysis
.
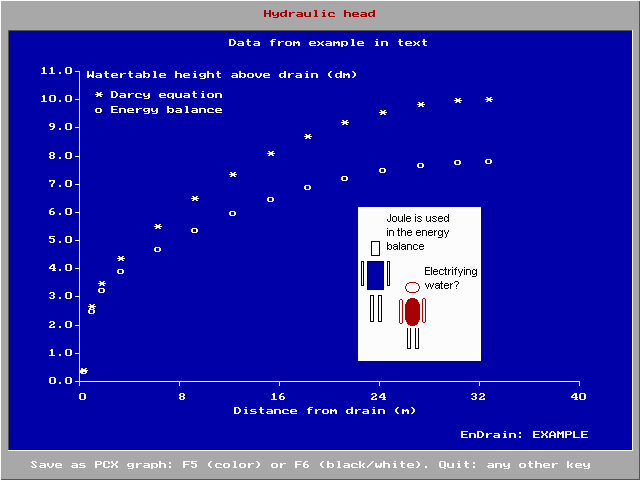
The blue figure shows an example of results of a computer aided calculation with the amplified drainage equation using the EnDrain program. It shows that incorporation of the incoming energy associated with the recharge leads to a somewhat deeper water table.
Drainage system (Agriculture)
An agricultural drainage system is a system by which the water level on or in the soil is controlled to enhance agricultural crop production.-Classification:Figure 1 classifies the various types of drainage systems...
, depth of the watertable, depth and hydraulic conductivity
Hydraulic conductivity
Hydraulic conductivity, symbolically represented as K, is a property of vascular plants, soil or rock, that describes the ease with which water can move through pore spaces or fractures. It depends on the intrinsic permeability of the material and on the degree of saturation...
of the soils. It is used in drainage
Drainage
Drainage is the natural or artificial removal of surface and sub-surface water from an area. Many agricultural soils need drainage to improve production or to manage water supplies.-Early history:...
design.
A well known steady-state drainage equation is the Hooghoudt drain spacing equation. Its original publication is in Dutch. The equation was introduced in the USA by van Schilfgaarde.
Hooghoudt's equation
Hooghoudt's equation can be written as:.- Q L2 = 8 Kb d (Di - Dd) (Dd - Dw) + 4 Ka (Dd - Dw)2
where:
- Q = steady stateSteady stateA system in a steady state has numerous properties that are unchanging in time. This implies that for any property p of the system, the partial derivative with respect to time is zero:...
drainage discharge rate (m/day) - Ka = hydraulic conductivityHydraulic conductivityHydraulic conductivity, symbolically represented as K, is a property of vascular plants, soil or rock, that describes the ease with which water can move through pore spaces or fractures. It depends on the intrinsic permeability of the material and on the degree of saturation...
of the soil above drain level (m/day) - Kb = hydraulic conductivityHydraulic conductivityHydraulic conductivity, symbolically represented as K, is a property of vascular plants, soil or rock, that describes the ease with which water can move through pore spaces or fractures. It depends on the intrinsic permeability of the material and on the degree of saturation...
of the soil below drain level (m/day) - Di = depth of the impermeable layer below drain level (m)
- Dd = depth of the drains (m)
- Dw = steady state depth of the watertable midway between the drains (m)
- L = spacing between the drains (m)
- d = equivalent depth, a function of L, (Di-Dd), and r
- r = drain radius (m)
Steady (equilibrium) state condition
In steady state
Steady state
A system in a steady state has numerous properties that are unchanging in time. This implies that for any property p of the system, the partial derivative with respect to time is zero:...
, the level of the water table remains constant and the discharge rate (Q) equals the rate of groundwater recharge (R), i.e. the amount of water entering the groundwater
Groundwater
Groundwater is water located beneath the ground surface in soil pore spaces and in the fractures of rock formations. A unit of rock or an unconsolidated deposit is called an aquifer when it can yield a usable quantity of water. The depth at which soil pore spaces or fractures and voids in rock...
through the watertable per unit of time. By considering a long-term (e.g. seasonal) average depth of the water table (Dw) in combination with the long-term average recharge rate (R), the net storage of water in that period of time is negligibly small and the steady state condition is satisfied: one obtains a dynamic equilibrium
Dynamic equilibrium
A dynamic equilibrium exists once a reversible reaction ceases to change its ratio of reactants/products, but substances move between the chemicals at an equal rate, meaning there is no net change. It is a particular example of a system in a steady state...
.
Derivation of the equation
For the derivation of the equation Hooghoudt used the law of Darcy
Darcy's law
Darcy's law is a phenomenologically derived constitutive equation that describes the flow of a fluid through a porous medium. The law was formulated by Henry Darcy based on the results of experiments on the flow of water through beds of sand...
, the summation of circular potential functions
Hydraulic head
Hydraulic head or piezometric head is a specific measurement of water pressure above a geodetic datum. It is usually measured as a water surface elevation, expressed in units of length, at the entrance of a piezometer...
and, for the determination of the influence of the impermeable layer, de method of mirror image
Mirror image
A mirror image is a reflected duplication of an object that appears identical but reversed. As an optical effect it results from reflection off of substances such as a mirror or water. It is also a concept in geometry and can be used as a conceptualization process for 3-D structures...
s and superposition
Superposition principle
In physics and systems theory, the superposition principle , also known as superposition property, states that, for all linear systems, the net response at a given place and time caused by two or more stimuli is the sum of the responses which would have been caused by each stimulus individually...
.
Hooghoudt published tables for the determination of the equivalent depth (d), because the function (F) in d = F (L,Di-Dd,r) consists of long series of terms.

- the discharge rate (Q) from the recharge rate (R) in a water balanceWater balanceIn hydrology, a water balance equation can be used to describe the flow of water in and out of a system. A system can be one of several hydrological domains, such as a column of soil or a drainage basin....
as detailed in the article: hydrology (agriculture)Hydrology (agriculture)Agricultural hydrology is the study of water balance components intervening in agricultural water management, notably in irrigation and drainage.-Water balance components:... - the permissible long term average depth of the water table (Dw) on the basis of agricultural drainage criteria
- the soil's hydraulic conductivityHydraulic conductivityHydraulic conductivity, symbolically represented as K, is a property of vascular plants, soil or rock, that describes the ease with which water can move through pore spaces or fractures. It depends on the intrinsic permeability of the material and on the degree of saturation...
(Ka and Kb) by measurements - the depth of the bottom of the aquiferAquiferAn aquifer is a wet underground layer of water-bearing permeable rock or unconsolidated materials from which groundwater can be usefully extracted using a water well. The study of water flow in aquifers and the characterization of aquifers is called hydrogeology...
(Di)
the design drain spacing (L) can be found from the equation in dependence of the drain depth (Dd) and drain radius (r).
Drainage criteria
One would not want the water table to be too shallow to avoid crop yield depression nor too deep to avoid drought conditions. This is a subject of drainage research
Drainage research
Drainage research is the study of agricultural drainage systems and their effects to arrive at optimal system design.- Aspects to be covered :...
. The figure shows that a seasonal average depth of the water table shallower than 70 cm causes a yield depression
The figure was made with the SegReg program for segmented regression
Segmented regression
Segmented regression is a method in regression analysis in which the independent variable is partitioned into intervals and a separate line segment is fit to each interval. Segmented or piecewise regression analysis can also be performed on multivariate data by partitioning the various independent...
.
Equivalent depth
In 1991 a closed-form expressionClosed-form expression
In mathematics, an expression is said to be a closed-form expression if it can be expressed analytically in terms of a bounded number of certain "well-known" functions...
was developed for the equivalent depth (d) that can replace the Hooghoudt tables :
- d = πL / 8 { ln(L/πr) + F(x) }
where:
- x = 2π (Di − Dd) / L
- F(x) = Σ 4e−2nx / n (1 − e−2nx) , with n = 1, 3, 5, . . .
Extended use
Theoretically, Hooghoudt's equation can also be used for sloping land. The theory on drainage of sloping land is corroborated by the results of sand tank experiments. In addition, the entrance resistance encountered by the water upon entering the drains can be accounted for.Amplification
The drainage formula can be amplified to account for (see figure on the right):- the additional energy associated with the incoming percolation water (recharge), see groundwater energy balanceGroundwater energy balanceThe groundwater energy balance is the energy balance of a groundwater body in terms of incoming hydraulic energy associated with groundwater inflow into the body, energy associated with the outflow, energy conversion into heat due to friction of flow, and the resulting change of energy status and...
- multiple soil layers
- anisotropricAnisotropyAnisotropy is the property of being directionally dependent, as opposed to isotropy, which implies identical properties in all directions. It can be defined as a difference, when measured along different axes, in a material's physical or mechanical properties An example of anisotropy is the light...
hydraulic conductivity, the vertical conductivity (Kv) being different from the horizontal (Kh) - drains of different dimensions with any width (W)

Computer program
The amplified drainage equation uses an hydraulic equivalent of Joule's lawJoule's law
Joule's laws are a pair of laws concerning the heat produced by a current and the energy dependence of an ideal gas to that of pressure, volume, and temperature, respectively...
in electricity.
It is in the form of a differential equation
Differential equation
A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...
that cannot be solved analytically (i.e. in a closed form
Closed-form expression
In mathematics, an expression is said to be a closed-form expression if it can be expressed analytically in terms of a bounded number of certain "well-known" functions...
) but the solution requires a numerical method for which a computer program
Computer program
A computer program is a sequence of instructions written to perform a specified task with a computer. A computer requires programs to function, typically executing the program's instructions in a central processor. The program has an executable form that the computer can use directly to execute...
is indispensable.
The availability of a computer program also helps in quickly assessing various alternatives and performing a sensitivity analysis
Sensitivity analysis
Sensitivity analysis is the study of how the variation in the output of a statistical model can be attributed to different variations in the inputs of the model. Put another way, it is a technique for systematically changing variables in a model to determine the effects of such changes.In any...
.
The blue figure shows an example of results of a computer aided calculation with the amplified drainage equation using the EnDrain program. It shows that incorporation of the incoming energy associated with the recharge leads to a somewhat deeper water table.
External links
- Website with free download of articles and software on land drainage: http://www.waterlog.info
- A chapter on agricultural drainage criteria: http://www.waterlog.info/pdf/chap17.pdf
- A chapter on determining hydraulic conductivity: http://www.waterlog.info/pdf/chap12.pdf

