Doob martingale
Encyclopedia
A Doob martingale is a mathematical construction of a stochastic process
which approximates a given random variable
and has the martingale property
with respect to the given filtration. It may be thought of as the evolving sequence of best approximations to the random variable based on information accumulated up to a certain time.
When analyzing sums, random walk
s, or other additive functions of independent random variables
, one can often apply the central limit theorem
, law of large numbers
, Chernoff's inequality, Chebyshev's inequality
or similar tools. When analyzing similar objects where the differences are not independent, the main tools are martingale
s and Azuma's inequality.
) is a generic construction that is always a martingale. Specifically, consider any set of random variables
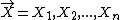
taking values in a set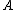
for which we are interested in the function 
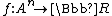and define:
where the above expectation is itself a random quantity since the expectation is only taken over
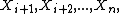
and
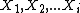
are treated as random variables. It is possible to show that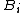
is always a martingale regardless of the properties of 
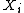. Thus if one can bound the differences
,
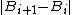one can apply Azuma's inequality and show that with high probability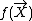
is concentrated around its expected value
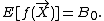
are independent and assume that
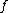satisfies
Stochastic process
In probability theory, a stochastic process , or sometimes random process, is the counterpart to a deterministic process...
which approximates a given random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
and has the martingale property
Martingale (probability theory)
In probability theory, a martingale is a model of a fair game where no knowledge of past events can help to predict future winnings. In particular, a martingale is a sequence of random variables for which, at a particular time in the realized sequence, the expectation of the next value in the...
with respect to the given filtration. It may be thought of as the evolving sequence of best approximations to the random variable based on information accumulated up to a certain time.
When analyzing sums, random walk
Random walk
A random walk, sometimes denoted RW, is a mathematical formalisation of a trajectory that consists of taking successive random steps. For example, the path traced by a molecule as it travels in a liquid or a gas, the search path of a foraging animal, the price of a fluctuating stock and the...
s, or other additive functions of independent random variables
Statistical independence
In probability theory, to say that two events are independent intuitively means that the occurrence of one event makes it neither more nor less probable that the other occurs...
, one can often apply the central limit theorem
Central limit theorem
In probability theory, the central limit theorem states conditions under which the mean of a sufficiently large number of independent random variables, each with finite mean and variance, will be approximately normally distributed. The central limit theorem has a number of variants. In its common...
, law of large numbers
Law of large numbers
In probability theory, the law of large numbers is a theorem that describes the result of performing the same experiment a large number of times...
, Chernoff's inequality, Chebyshev's inequality
Chebyshev's inequality
In probability theory, Chebyshev’s inequality guarantees that in any data sample or probability distribution,"nearly all" values are close to the mean — the precise statement being that no more than 1/k2 of the distribution’s values can be more than k standard deviations away from the mean...
or similar tools. When analyzing similar objects where the differences are not independent, the main tools are martingale
Martingale (probability theory)
In probability theory, a martingale is a model of a fair game where no knowledge of past events can help to predict future winnings. In particular, a martingale is a sequence of random variables for which, at a particular time in the realized sequence, the expectation of the next value in the...
s and Azuma's inequality.
Definition
A Doob martingale (named after J. L. DoobJoseph Leo Doob
Joseph Leo Doob was an American mathematician, specializing in analysis and probability theory.The theory of martingales was developed by Doob.-Early life and education:...
) is a generic construction that is always a martingale. Specifically, consider any set of random variables
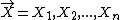
taking values in a set
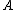for which we are interested in the function 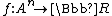and define:where the above expectation is itself a random quantity since the expectation is only taken over
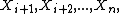
and
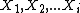
are treated as random variables. It is possible to show that
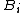is always a martingale regardless of the properties of 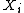. Thus if one can bound the differences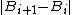,one can apply Azuma's inequality and show that with high probability
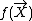is concentrated around its expected value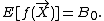McDiarmid's inequality
One common way of bounding the differences and applying Azuma's inequality to a Doob martingale is called McDiarmid's inequality. Suppose are independent and assume that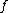 satisfies-
(In other words, replacing the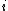
-th coordinate 
by some other value changes the value of 
by at most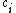
.)
It follows that
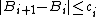
and therefore Azuma's inequality yields the following McDiarmid inequalities for any
:
-
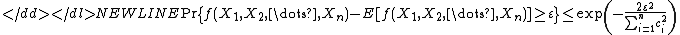
and
-
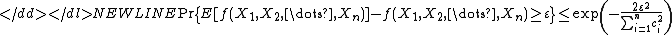
and
-
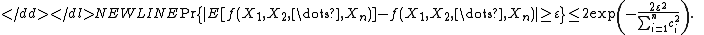
See also
- Markov inequality
- Chebyshev's inequalityChebyshev's inequalityIn probability theory, Chebyshev’s inequality guarantees that in any data sample or probability distribution,"nearly all" values are close to the mean — the precise statement being that no more than 1/k2 of the distribution’s values can be more than k standard deviations away from the mean...
- Bernstein inequalities (probability theory)
-
-
-