Dominance (game theory)
Encyclopedia
In game theory
, strategic dominance (commonly called simply dominance) occurs when one strategy
is better than another strategy for one player, no matter how that player's opponents may play. Many simple games can be solved using dominance.
The opposite, intransitivity
, occurs in games where one strategy may be better or worse than another strategy for one player, depending on how the player's opponents may play.
The result of the comparison is one of:
This notion can be generalized beyond the comparison of two strategies.
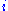, a strategy 
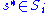weakly dominates another strategy 
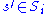if
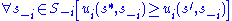(With at least one 
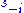that gives a strict inequality)
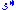strictly dominates 
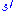if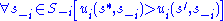
where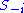
represents the product of all strategy sets other than player 
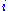's
If a strictly dominant strategy exists for one player in a game, that player will play that strategy in each of the game's Nash equilibria
. If both players have a strictly dominant strategy, the game has only one unique Nash equilibrium. However, that Nash equilibrium is not necessarily Pareto optimal, meaning that there may be non-equilibrium outcomes of the game that would be better for both players. The classic game used to illustrate this is the Prisoner's Dilemma
.
Strictly dominated strategies cannot be a part of a Nash equilibrium, and as such, it is irrational for any player to play them. On the other hand, weakly dominated strategies may be part of Nash equilibria. For instance, consider the payoff matrix pictured at the right.
Strategy C weakly dominates strategy D. Consider playing C: If one's opponent plays C, one gets 1; if one's opponent plays D, one gets 0. Compare this to D, where one gets 0 regardless. Since in one case, one does better by playing C instead of D and never does worse, C weakly dominates D. Despite this, (D, D) is a Nash equilibrium. Suppose both players choose D. Neither player will do any better by unilaterally deviating—if a player switches to playing C, they will still get 0. This satisfies the requirements of a Nash equilibrium. Suppose both players choose C. Neither player will do better by unilaterally deviating—if a player switches to playing D, they will get 0. This also satisfies the requirements of a Nash equilibrium.
removing dominated strategies. In the first step, at most one dominated strategy is removed from the strategy space of each of the players since no rational player would ever play these strategies. This results in a new, smaller game. Some strategies—that were not dominated before—may be dominated in the smaller game. The first step is repeated, creating a new even smaller game, and so on. It is possible that in any step 0 strategies may be deleted for some players. The process stops when in any round 0 strategies are deleted. This process is valid since it is assumed that rationality among players is common knowledge
, that is, each player knows that the rest of the players are rational, and each player knows that the rest of the players know that he knows that the rest of the players are rational, and so on ad infinitum (see Aumann, 1976).
There are two versions of this process.
One version involves only eliminating strictly dominated strategies. If, after completing this process, there is only one strategy for each player remaining, that strategy set is the unique Nash equilibrium.
Another version involves eliminating both strictly and weakly dominated strategies. If, at the end of the process, there is a single strategy for each player, this strategy set is also a Nash equilibrium
. However, unlike the first process, elimination of weakly dominated strategies may eliminate some Nash equilibria. As a result, the Nash equilibrium found by eliminating weakly dominated strategies may not be the only Nash equilibrium. (In some games, if we remove weakly dominated strategies in a different order, we may end up with a different Nash equilibrium.)
In any case, if by iterated elimination of dominated strategies there is only one strategy left for each player, the game is called a dominant solvable game.
Game theory
Game theory is a mathematical method for analyzing calculated circumstances, such as in games, where a person’s success is based upon the choices of others...
, strategic dominance (commonly called simply dominance) occurs when one strategy
Strategy (game theory)
In game theory, a player's strategy in a game is a complete plan of action for whatever situation might arise; this fully determines the player's behaviour...
is better than another strategy for one player, no matter how that player's opponents may play. Many simple games can be solved using dominance.
The opposite, intransitivity
Intransitivity
In mathematics, the term intransitivity is used for related, but different, properties of binary relations:- Intransitivity :A relation is transitive if, whenever it relates some A to some B, and that B to some C, it also relates that A to that C...
, occurs in games where one strategy may be better or worse than another strategy for one player, depending on how the player's opponents may play.
Terminology
When a player tries to choose the "best" strategy among a multitude of options, that player may compare two strategies A and B to see which one is better.The result of the comparison is one of:
- B dominates A: choosing B always gives at least as good an outcome as choosing A. There are 2 possibilities:
- B strictly dominates A: choosing B always gives a better outcome than choosing A, no matter what the other player(s) do.
- B weakly dominates A: There is at least one set of opponents' action for which B is superior, and all other sets of opponents' actions give B at least the same payoff as A.
- B and A are intransitive: B neither dominates, nor is dominated by, A. Choosing A is better in some cases, while choosing B is better in other cases, depending on exactly how the opponent chooses to play. For example, B is "throw rock" while A is "throw scissors" in Rock, Paper, ScissorsRock, Paper, ScissorsRock-paper-scissors is a hand game played by two people. The game is also known as roshambo, or another ordering of the three items ....
. - B is dominated by A: choosing B never gives a better outcome than choosing A, no matter what the other player(s) do. There are 2 possibilities:
- B is weakly dominated by A: There is at least one set of opponents' actions for which B gives a worse outcome than A, while all other sets of opponents' actions give A at least the same payoff as B. (Strategy A weakly dominates B).
- B is strictly dominated by A: choosing B always gives a worse outcome than choosing A, no matter what the other player(s) do. (Strategy A strictly dominates B).
This notion can be generalized beyond the comparison of two strategies.
- Strategy B is strictly dominant if strategy B strictly dominates every other possible strategy.
- Strategy B is weakly dominant if strategy B dominates all other strategies, but some are only weakly dominated.
- Strategy B is strictly dominated if some other strategy exists that strictly dominates B.
- Strategy B is weakly dominated if some other strategy exists that weakly dominates B.
Mathematical definition
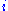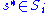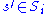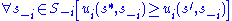For any player, a strategy weakly dominates another strategy if (With at least one 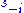that gives a strict inequality) 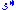strictly dominates 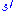if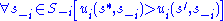where
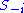represents the product of all strategy sets other than player 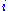'sDominance and Nash equilibria
| C | D | |
|---|---|---|
| C | 1, 1 | 0, 0 |
| D | 0, 0 | 0, 0 |
If a strictly dominant strategy exists for one player in a game, that player will play that strategy in each of the game's Nash equilibria
Nash equilibrium
In game theory, Nash equilibrium is a solution concept of a game involving two or more players, in which each player is assumed to know the equilibrium strategies of the other players, and no player has anything to gain by changing only his own strategy unilaterally...
. If both players have a strictly dominant strategy, the game has only one unique Nash equilibrium. However, that Nash equilibrium is not necessarily Pareto optimal, meaning that there may be non-equilibrium outcomes of the game that would be better for both players. The classic game used to illustrate this is the Prisoner's Dilemma
Prisoner's dilemma
The prisoner’s dilemma is a canonical example of a game, analyzed in game theory that shows why two individuals might not cooperate, even if it appears that it is in their best interest to do so. It was originally framed by Merrill Flood and Melvin Dresher working at RAND in 1950. Albert W...
.
Strictly dominated strategies cannot be a part of a Nash equilibrium, and as such, it is irrational for any player to play them. On the other hand, weakly dominated strategies may be part of Nash equilibria. For instance, consider the payoff matrix pictured at the right.
Strategy C weakly dominates strategy D. Consider playing C: If one's opponent plays C, one gets 1; if one's opponent plays D, one gets 0. Compare this to D, where one gets 0 regardless. Since in one case, one does better by playing C instead of D and never does worse, C weakly dominates D. Despite this, (D, D) is a Nash equilibrium. Suppose both players choose D. Neither player will do any better by unilaterally deviating—if a player switches to playing C, they will still get 0. This satisfies the requirements of a Nash equilibrium. Suppose both players choose C. Neither player will do better by unilaterally deviating—if a player switches to playing D, they will get 0. This also satisfies the requirements of a Nash equilibrium.
Iterated elimination of dominated strategies (IEDS)
The iterated elimination (or deletion) of dominated strategies is one common technique for solving games that involves iterativelyIteration
Iteration means the act of repeating a process usually with the aim of approaching a desired goal or target or result. Each repetition of the process is also called an "iteration," and the results of one iteration are used as the starting point for the next iteration.-Mathematics:Iteration in...
removing dominated strategies. In the first step, at most one dominated strategy is removed from the strategy space of each of the players since no rational player would ever play these strategies. This results in a new, smaller game. Some strategies—that were not dominated before—may be dominated in the smaller game. The first step is repeated, creating a new even smaller game, and so on. It is possible that in any step 0 strategies may be deleted for some players. The process stops when in any round 0 strategies are deleted. This process is valid since it is assumed that rationality among players is common knowledge
Common knowledge (logic)
Common knowledge is a special kind of knowledge for a group of agents. There is common knowledge of p in a group of agents G when all the agents in G know p, they all know that they know p, they all know that they all know that they know p, and so on ad infinitum.The concept was first introduced in...
, that is, each player knows that the rest of the players are rational, and each player knows that the rest of the players know that he knows that the rest of the players are rational, and so on ad infinitum (see Aumann, 1976).
There are two versions of this process.
One version involves only eliminating strictly dominated strategies. If, after completing this process, there is only one strategy for each player remaining, that strategy set is the unique Nash equilibrium.
Another version involves eliminating both strictly and weakly dominated strategies. If, at the end of the process, there is a single strategy for each player, this strategy set is also a Nash equilibrium
Nash equilibrium
In game theory, Nash equilibrium is a solution concept of a game involving two or more players, in which each player is assumed to know the equilibrium strategies of the other players, and no player has anything to gain by changing only his own strategy unilaterally...
. However, unlike the first process, elimination of weakly dominated strategies may eliminate some Nash equilibria. As a result, the Nash equilibrium found by eliminating weakly dominated strategies may not be the only Nash equilibrium. (In some games, if we remove weakly dominated strategies in a different order, we may end up with a different Nash equilibrium.)
In any case, if by iterated elimination of dominated strategies there is only one strategy left for each player, the game is called a dominant solvable game.