
Doléans-Dade exponential
Encyclopedia
In stochastic calculus
, the Doléans-Dade exponential, Doléans exponential, or stochastic exponential, of a semimartingale
X is defined to be the solution to the stochastic differential equation
with initial condition . The concept is named after Catherine Doléans-Dade. It is sometimes denoted by (X).
In the case where X is differentiable, then Y is given by the differential equation to which the solution is .
Alternatively, if for a Brownian motion
B, then the Doléans-Dade exponential is a geometric Brownian motion
. For any continuous semimartingale X, applying Itō's lemma
with gives
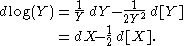
Exponentiating gives the solution
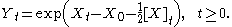
This differs from what might be expected by comparison with the case where X is differentiable due to the existence of the quadratic variation
term[ X] in the solution.
The Doléans-Dade exponential is useful in the case when X is a local martingale
. Then, (X) will also be a local martingale whereas the normal exponential exp(X) is not. This is used in the Girsanov theorem
. Criteria for a continuous local martingale X to ensure that its stochastic exponential (X) is actually a (uniformly integrable) martingale
are given by Kazamaki's condition
, Novikov's condition
and Beneš' condition.
It is possible to apply Itō's lemma for non-continuous semimartingales in a similar way to show that the Doléans-Dade exponential of any semimartingale X is

where the product extents over the (countable many) jumps of X up to time t.
Stochastic calculus
Stochastic calculus is a branch of mathematics that operates on stochastic processes. It allows a consistent theory of integration to be defined for integrals of stochastic processes with respect to stochastic processes...
, the Doléans-Dade exponential, Doléans exponential, or stochastic exponential, of a semimartingale
Semimartingale
In probability theory, a real valued process X is called a semimartingale if it can be decomposed as the sum of a local martingale and an adapted finite-variation process....
X is defined to be the solution to the stochastic differential equation
Stochastic differential equation
A stochastic differential equation is a differential equation in which one or more of the terms is a stochastic process, thus resulting in a solution which is itself a stochastic process....
with initial condition . The concept is named after Catherine Doléans-Dade. It is sometimes denoted by (X).
In the case where X is differentiable, then Y is given by the differential equation to which the solution is .
Alternatively, if for a Brownian motion
Wiener process
In mathematics, the Wiener process is a continuous-time stochastic process named in honor of Norbert Wiener. It is often called standard Brownian motion, after Robert Brown...
B, then the Doléans-Dade exponential is a geometric Brownian motion
Geometric Brownian motion
A geometric Brownian motion is a continuous-time stochastic process in which the logarithm of the randomly varying quantity follows a Brownian motion, also called a Wiener process...
. For any continuous semimartingale X, applying Itō's lemma
Ito's lemma
In mathematics, Itō's lemma is used in Itō stochastic calculus to find the differential of a function of a particular type of stochastic process. It is named after its discoverer, Kiyoshi Itō...
with gives
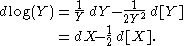
Exponentiating gives the solution
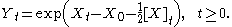
This differs from what might be expected by comparison with the case where X is differentiable due to the existence of the quadratic variation
Quadratic variation
In mathematics, quadratic variation is used in the analysis of stochastic processes such as Brownian motion and martingales. Quadratic variation is just one kind of variation of a process.- Definition :...
term
The Doléans-Dade exponential is useful in the case when X is a local martingale
Local martingale
In mathematics, a local martingale is a type of stochastic process, satisfying the localized version of the martingale property. Every martingale is a local martingale; every bounded local martingale is a martingale; however, in general a local martingale is not a martingale, because its...
. Then, (X) will also be a local martingale whereas the normal exponential exp(X) is not. This is used in the Girsanov theorem
Girsanov theorem
In probability theory, the Girsanov theorem describes how the dynamics of stochastic processes change when the original measure is changed to an equivalent probability measure...
. Criteria for a continuous local martingale X to ensure that its stochastic exponential (X) is actually a (uniformly integrable) martingale
Martingale (probability theory)
In probability theory, a martingale is a model of a fair game where no knowledge of past events can help to predict future winnings. In particular, a martingale is a sequence of random variables for which, at a particular time in the realized sequence, the expectation of the next value in the...
are given by Kazamaki's condition
Kazamaki's condition
Kazamaki's condition gives a sufficient criterion ensuring that the Doléans-Dade exponential of a local martingale is a true martingale. In mathematics, this is particularly important if one wishes to apply Girsanov's theorem in order to perform a change of measure...
, Novikov's condition
Novikov's condition
In probability theory, Novikov's condition is the sufficient condition for a stochastic process which takes the form of the Radon-Nikodym derivative in Girsanov's theorem to be a martingale...
and Beneš' condition.
It is possible to apply Itō's lemma for non-continuous semimartingales in a similar way to show that the Doléans-Dade exponential of any semimartingale X is

where the product extents over the (countable many) jumps of X up to time t.

