
Discrete q-Hermite polynomials
Encyclopedia
In mathematics, the discrete q-Hermite polynomials are two closely related families hn(x;q) and ĥn(x;q) of basic hypergeometric orthogonal polynomials
in the basic Askey scheme
, introduced by . give a detailed list of their properties.
by
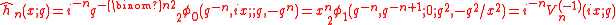
and are related by
Orthogonal polynomials
In mathematics, the classical orthogonal polynomials are the most widely used orthogonal polynomials, and consist of the Hermite polynomials, the Laguerre polynomials, the Jacobi polynomials together with their special cases the ultraspherical polynomials, the Chebyshev polynomials, and the...
in the basic Askey scheme
Askey scheme
In mathematics, the Askey scheme is a way of organizing orthogonal polynomials of hypergeometric or basic hypergeometric type into a hierarchy. For the classical orthogonal polynomials discussed in , the Askey scheme was first drawn by and by , and has since been extended by and to cover basic...
, introduced by . give a detailed list of their properties.
Definition
The discrete q-Hermite polynomials are given in terms of basic hypergeometric functions and the Al-Salam–Carlitz polynomialsAl-Salam–Carlitz polynomials
In mathematics, Al-Salam–Carlitz polynomials U and V are two families of basic hypergeometric orthogonal polynomials in the basic Askey scheme, introduced by...
by

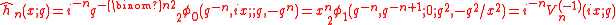
and are related by


