
Dirichlet algebra
Encyclopedia
In mathematics
, a Dirichlet algebra is a particular type of algebra associated to a compact Hausdorff space X. It is a closed subalgebra of C(X), the uniform algebra
of bounded continuous functions on X, whose real parts are dense in the algebra of bounded continuous real functions on X. The concept was introduced by .
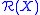 be the set of all rational function
be the set of all rational function
s that are continuous on ; in other words functions that have no poles in
; in other words functions that have no poles in  . Then
. Then
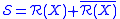
is a *-subalgebra of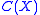 , and of
, and of 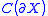 . If
. If 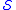 is dense
is dense
in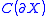 , we say
, we say 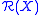 is a Dirichlet algebra.
is a Dirichlet algebra.
It can be shown that if an operator has
has  as a spectral set, and
as a spectral set, and 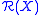 is a Dirichlet algebra, then
is a Dirichlet algebra, then  has a normal boundary dilation. This generalises Sz.-Nagy's dilation theorem
has a normal boundary dilation. This generalises Sz.-Nagy's dilation theorem
, which can be seen as a consequence of this by letting

Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a Dirichlet algebra is a particular type of algebra associated to a compact Hausdorff space X. It is a closed subalgebra of C(X), the uniform algebra
Uniform algebra
A uniform algebra A on a compact Hausdorff topological space X is a closed subalgebra of the C*-algebra C with the following properties:As a closed subalgebra of the commutative Banach algebra C a uniform algebra is itself a unital commutative Banach algebra A uniform algebra A on a compact...
of bounded continuous functions on X, whose real parts are dense in the algebra of bounded continuous real functions on X. The concept was introduced by .
Example
Let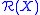 be the set of all rational function
be the set of all rational functionRational function
In mathematics, a rational function is any function which can be written as the ratio of two polynomial functions. Neither the coefficients of the polynomials nor the values taken by the function are necessarily rational.-Definitions:...
s that are continuous on
 ; in other words functions that have no poles in
; in other words functions that have no poles in  . Then
. Then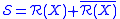
is a *-subalgebra of
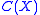 , and of
, and of 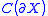 . If
. If 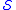 is dense
is denseDense set
In topology and related areas of mathematics, a subset A of a topological space X is called dense if any point x in X belongs to A or is a limit point of A...
in
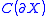 , we say
, we say 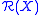 is a Dirichlet algebra.
is a Dirichlet algebra.It can be shown that if an operator
 has
has  as a spectral set, and
as a spectral set, and 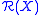 is a Dirichlet algebra, then
is a Dirichlet algebra, then  has a normal boundary dilation. This generalises Sz.-Nagy's dilation theorem
has a normal boundary dilation. This generalises Sz.-Nagy's dilation theoremSz.-Nagy's dilation theorem
The Sz.-Nagy dilation theorem states that every contraction T on a Hilbert space H has a unitary dilation U to a Hilbert space K, containing H, withT^n = P_H U^n \vert_H,\quad n\ge 0....
, which can be seen as a consequence of this by letting


