
Spectral set
Encyclopedia
In operator theory, a set  is said to be a spectral set for a (possibly unbounded) linear operator
is said to be a spectral set for a (possibly unbounded) linear operator  on a Banach space if the spectrum of
on a Banach space if the spectrum of  is in
is in  and von-Neumann's inequality holds for
and von-Neumann's inequality holds for  on
on  - i.e. for all rational functions
- i.e. for all rational functions 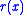 with no poles on
with no poles on 

This concept is related to the topic of analytic functional calculus
of operators. In general, one want to get more details about the operators constructed from functions with the original operator as the variable.
 is said to be a spectral set for a (possibly unbounded) linear operator
is said to be a spectral set for a (possibly unbounded) linear operator  on a Banach space if the spectrum of
on a Banach space if the spectrum of  is in
is in  and von-Neumann's inequality holds for
and von-Neumann's inequality holds for  on
on  - i.e. for all rational functions
- i.e. for all rational functions 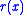 with no poles on
with no poles on 

This concept is related to the topic of analytic functional calculus
of operators. In general, one want to get more details about the operators constructed from functions with the original operator as the variable.

