Dini continuity
Encyclopedia
In mathematical analysis
, Dini continuity is a refinement of continuity
.
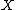be a compact
subset of a metric space (such as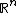
), and let 
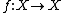be a function from 
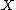into itself. The modulus of continuity
of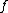
is
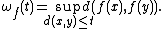
The function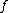
is called Dini-continuous if
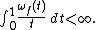
An equivalent condition is that, for any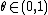
,
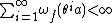
where
is the diameter of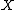 
.
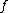is Dini continuous then it is continuous.
If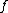
is Lipschitz continuous then it is Dini continuous.
Mathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
, Dini continuity is a refinement of continuity
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
.
Definition
Let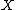 be a compactCompact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
subset of a metric space (such as
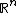), and let 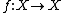be a function from 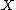into itself. The modulus of continuityModulus of continuity
In mathematical analysis, a modulus of continuity is a function\omega:[0,\infty]\to[0,\infty]used to measure quantitatively the uniform continuity of functions. So, a function f:I\to\R admits \omega as a modulus of continuity if and only if|f-f|\leq\omega,for all x and y in the domain of f...
of
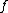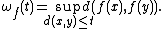
isThe function
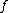is called Dini-continuous if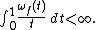An equivalent condition is that, for any
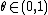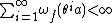
,where
is the diameter of 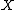.Properties
If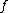 is Dini continuous then it is continuous.If
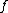is Lipschitz continuous then it is Dini continuous.See also
- Dini testDini testIn mathematics, the Dini and Dini-Lipschitz tests are highly precise tests that can be used to prove that the Fourier series of a function converges at a given point. These tests are named after Ulisse Dini and Rudolf Lipschitz.- Definition :...
-- a condition similar to local Dini continuity implies convergence of a Fourier transformFourier transformIn mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
.