Dependency network
Encyclopedia
The dependency network approach provides a new system level analysis of the activity and topology of directed networks. The approach extracts causal topological relations between the networks nodes (when the network structure is analyzed), and provides an important step towards inference of causal activity relations between the network nodes (when analyzing the network activity). This methodology has originally been introduced for the study of financial data, it has been extended and applied to other systems, such as the immune system
, and semantic networks.
In the case of network activity, the analysis is based on partial correlation
s, which are becoming ever more widely used to investigate complex systems
. In simple words, the partial (or residual) correlation
is a measure of the effect (or contribution) of a given node, say j, on the correlations between another pair of nodes, say i and k. Using this concept, the dependency of one node on another node, is calculated for the entire network. This results in a directed weighted adjacency matrix, of a fully connected network. Once the adjacency matrix has been constructed, different algorithms can be used to construct the network, such as a threshold network, Minimal Spanning Tree (MST), Planar Maximally Filtered Graph (PMFG), and others.
This original methodology was first presented at the end of 2010, published in the highly cited PLoS ONE
journal. This research, headed by Dror Y. Kenett and his Ph.D. supervisor Prof. Eshel Ben-Jacob
, collaborated with Dr. Michele Tumminello and Prof. Rosario Mantegna. They quantitatively uncovered hidden information about the underlying structure of the U.S. stock market
, information that was not present in the standard correlation
networks. One of the main results of this work is that for the investigated time period (2001–2003), the structure of the network is dominated by companies belonging to the Financial sector, which are the hubs in the Dependency network. Thus, they were able for the first time to quantitatively show the dependency relationships between the different economic sectors. Following this work, the Dependency network methodology has been applied to the study of the Immune System
, and semantic networks. As such, this methodology is applicable to any complex system
.
. Therefore, we define the influence of node j on node i, or the dependency
of node i on node j- D(i,j), to be the sum of the influence of node j on the correlations of node i with all other nodes.
In the case of network topology, the analysis is based on the effect of node deletion on the shortest paths between the network nodes. More specifically, we define the influence of node j on each pair of nodes (i,k) to be the inverse of the topological distance between these nodes in the presence of j minus the inverse distance between them in the absence of node j. Then we define the influence of node j on node i, or the dependency of node i on node j - D(i,j), to be the sum of the influence of node j on the distances between node i with all other nodes k.
:
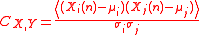
Where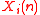
and 
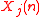are the activity of nodes i and j of subject n, μ stands for average, and sigma the STD of the dynamics profiles of nodes i and j. Note that the node-node correlations (or for simplicity the node correlations) for all pairs of nodes define a symmetric correlation matrix whose 
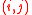element is the correlation between nodes i and j.
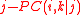is defined as:
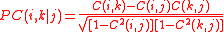
where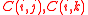
and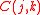 
are the node correlations defined above.
and 
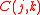of node j on the correlation C(i,k) is given by:
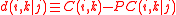
This avoids the trivial case were node j appears to strongly effect the correlation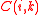
, mainly because 
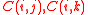and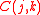 
have small values. We note that this quantity can be viewed either as the correlation dependency of C(i,k) on node j, (the term used here) or as the correlation influence of node j on the correlation C(i,k).
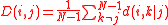
As defined,D(i,j) is a measure of the average influence of node j on the correlations C(i,k) over all nodes k not equal to j. The node activity dependencies define a dependency matrix D whose (i,j) element is the dependency of node i on node j. It is important to note that while the correlation matrix C is a symmetric matrix, the dependency matrix D is nonsymmetrical –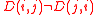
since the influence of node j on node i is not equal to the influence of node i on node j. For this reason, some of the methods used in the analyses of the correlation matrix (e.g. the PCA) have to be replaced or are less efficient. Yet there are other methods, as the ones used here, that can properly account for the non-symmetric nature of the dependency matrix.
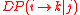- the shortest topological path with each segment corresponds to a distance 1, between nodes i and k is given:
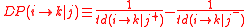
Where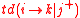
and 
are the shortest directed topological path from node i to node k in the presence and the absence of node j respectively.
As defined, D(i,j) is a measure of the average influence of node j on the directed paths from node i to all other nodes k. The node structural dependencies define a dependency matrix D whose (i,j) element is the dependency of node i on node j, or the influence of node j on node i. It is important to note that the dependency matrix D is nonsymmetrical –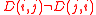
since the influence of node j on node i is not equal to the influence of node i on node j.
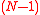edges with no loops while the PMFG sub-graph contains 
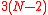edges.
Immune system
An immune system is a system of biological structures and processes within an organism that protects against disease by identifying and killing pathogens and tumor cells. It detects a wide variety of agents, from viruses to parasitic worms, and needs to distinguish them from the organism's own...
, and semantic networks.
In the case of network activity, the analysis is based on partial correlation
Partial correlation
In probability theory and statistics, partial correlation measures the degree of association between two random variables, with the effect of a set of controlling random variables removed.-Formal definition:...
s, which are becoming ever more widely used to investigate complex systems
Complex systems
Complex systems present problems in mathematical modelling.The equations from which complex system models are developed generally derive from statistical physics, information theory and non-linear dynamics, and represent organized but unpredictable behaviors of systems of nature that are considered...
. In simple words, the partial (or residual) correlation
Correlation
In statistics, dependence refers to any statistical relationship between two random variables or two sets of data. Correlation refers to any of a broad class of statistical relationships involving dependence....
is a measure of the effect (or contribution) of a given node, say j, on the correlations between another pair of nodes, say i and k. Using this concept, the dependency of one node on another node, is calculated for the entire network. This results in a directed weighted adjacency matrix, of a fully connected network. Once the adjacency matrix has been constructed, different algorithms can be used to construct the network, such as a threshold network, Minimal Spanning Tree (MST), Planar Maximally Filtered Graph (PMFG), and others.
Importance
The partial correlation based Dependency Networks is a revolutionary new class of correlation based networks, which is capable of uncovering hidden relationships between the nodes of the network.This original methodology was first presented at the end of 2010, published in the highly cited PLoS ONE
PLoS ONE
PLoS ONE is an open access peer-reviewed scientific journal published by the Public Library of Science since 2006. It covers primary research from any discipline within science and medicine. All submissions go through an internal and external pre-publication peer review but are not excluded on the...
journal. This research, headed by Dror Y. Kenett and his Ph.D. supervisor Prof. Eshel Ben-Jacob
Eshel Ben-Jacob
Eshel Ben-Jacob , is a theoretical and experimental physicist at Tel Aviv University, holder of the Maguy-Glass Chair in Physics of Complex Systems, and Fellow of the Center for Theoretical Biological Physics at the University of California San Diego...
, collaborated with Dr. Michele Tumminello and Prof. Rosario Mantegna. They quantitatively uncovered hidden information about the underlying structure of the U.S. stock market
New York Stock Exchange
The New York Stock Exchange is a stock exchange located at 11 Wall Street in Lower Manhattan, New York City, USA. It is by far the world's largest stock exchange by market capitalization of its listed companies at 13.39 trillion as of Dec 2010...
, information that was not present in the standard correlation
Correlation
In statistics, dependence refers to any statistical relationship between two random variables or two sets of data. Correlation refers to any of a broad class of statistical relationships involving dependence....
networks. One of the main results of this work is that for the investigated time period (2001–2003), the structure of the network is dominated by companies belonging to the Financial sector, which are the hubs in the Dependency network. Thus, they were able for the first time to quantitatively show the dependency relationships between the different economic sectors. Following this work, the Dependency network methodology has been applied to the study of the Immune System
Immune system
An immune system is a system of biological structures and processes within an organism that protects against disease by identifying and killing pathogens and tumor cells. It detects a wide variety of agents, from viruses to parasitic worms, and needs to distinguish them from the organism's own...
, and semantic networks. As such, this methodology is applicable to any complex system
Complex system
A complex system is a system composed of interconnected parts that as a whole exhibit one or more properties not obvious from the properties of the individual parts....
.
Overview
To be more specific, the partial correlations of the pair, given j is the correlations between them after proper subtraction of the correlations between i and j and between k and j. Defined this way, the difference between the correlations and the partial correlations provides a measure of the influence of node j on the correlationCorrelation
In statistics, dependence refers to any statistical relationship between two random variables or two sets of data. Correlation refers to any of a broad class of statistical relationships involving dependence....
. Therefore, we define the influence of node j on node i, or the dependency
Dependency
Dependency or dependent may refer to:-Computer science:*dependency, also called Coupling , a state in which one object uses a functionality of another object...
of node i on node j- D(i,j), to be the sum of the influence of node j on the correlations of node i with all other nodes.
In the case of network topology, the analysis is based on the effect of node deletion on the shortest paths between the network nodes. More specifically, we define the influence of node j on each pair of nodes (i,k) to be the inverse of the topological distance between these nodes in the presence of j minus the inverse distance between them in the absence of node j. Then we define the influence of node j on node i, or the dependency of node i on node j - D(i,j), to be the sum of the influence of node j on the distances between node i with all other nodes k.
The node-node correlations
The node=node correlations can be calculated by Pearson’s formulaPearson product-moment correlation coefficient
In statistics, the Pearson product-moment correlation coefficient is a measure of the correlation between two variables X and Y, giving a value between +1 and −1 inclusive...
:
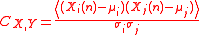
Where
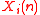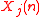and are the activity of nodes i and j of subject n, μ stands for average, and sigma the STD of the dynamics profiles of nodes i and j. Note that the node-node correlations (or for simplicity the node correlations) for all pairs of nodes define a symmetric correlation matrix whose 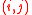element is the correlation between nodes i and j.Partial correlations
Next we use the resulting node correlations to compute the partial correlations. The first order partial correlation coefficient is a statistical measure indicating how a third variable affects the correlation between two other variables. The partial correlation between nodes i and k with respect to a third node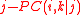 is defined as: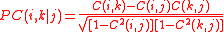where
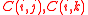and 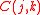are the node correlations defined above.The correlation influence and correlation dependency
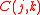The relative effect of the correlations and of node j on the correlation C(i,k) is given by: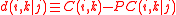This avoids the trivial case were node j appears to strongly effect the correlation
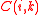, mainly because 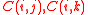and 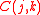have small values. We note that this quantity can be viewed either as the correlation dependency of C(i,k) on node j, (the term used here) or as the correlation influence of node j on the correlation C(i,k).Node activity dependencies
Next, we define the total influence of node j on node i, or the dependency D(i,j) of node i on node j to be: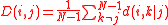As defined,D(i,j) is a measure of the average influence of node j on the correlations C(i,k) over all nodes k not equal to j. The node activity dependencies define a dependency matrix D whose (i,j) element is the dependency of node i on node j. It is important to note that while the correlation matrix C is a symmetric matrix, the dependency matrix D is nonsymmetrical –
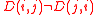since the influence of node j on node i is not equal to the influence of node i on node j. For this reason, some of the methods used in the analyses of the correlation matrix (e.g. the PCA) have to be replaced or are less efficient. Yet there are other methods, as the ones used here, that can properly account for the non-symmetric nature of the dependency matrix.The structure dependency networks
The path influence and distance dependency: The relative effect of node j on the directed path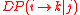 - the shortest topological path with each segment corresponds to a distance 1, between nodes i and k is given: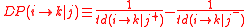Where
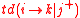and are the shortest directed topological path from node i to node k in the presence and the absence of node j respectively.Node structural dependencies
Next, we define the total influence of node j on node i, or the dependency D(i,j) of node i on node j to be:As defined, D(i,j) is a measure of the average influence of node j on the directed paths from node i to all other nodes k. The node structural dependencies define a dependency matrix D whose (i,j) element is the dependency of node i on node j, or the influence of node j on node i. It is important to note that the dependency matrix D is nonsymmetrical –
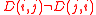since the influence of node j on node i is not equal to the influence of node i on node j.Visualization of the Dependency Network
The Dependency matrix is the weighted adjacency matrix, representing the fully connected network. Different algorithms can be applied to filter the fully connected network to obtain the most meaningful information, such as using a threshold approach, or different pruning algorithms. A widely used method to construct informative sub-graph of a complete network is the Minimum Spanning Tree (MST). Another informative sub-graph, which retains more information (in comparison to the MST) is the Planar Maximally Filtered Graph (PMFG) which is used here. Both methods are based on hierarchical clustering and the resulting sub-graphs include all the N nodes in the network whose edges represent the most relevant association correlations. The MST sub-graph contains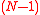edges with no loops while the PMFG sub-graph contains 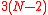edges.