Density matrix renormalization group
Encyclopedia
The density matrix renormalization group (DMRG) is a numerical variational technique devised to obtain the low energy physics of quantum
many-body systems with high accuracy. It was invented in 1992 by Steven R. White
and it is nowadays the most efficient method for 1-dimensional systems.
many-body physics is the fact that the Hilbert space grows exponentially with size. For example, a spin-1/2 chain of length L has 2 L degrees of freedom. The DMRG is an iterative, variational method that reduces effective degrees of freedom to those most important for a target state. The target state is often the ground state.
After a warmup cycle, the method splits the system into two blocks, which need not have equal sizes, and two sites in between. A set of representative states has been chosen for the block during the warmup. This set of left block + two sites + right block is known as the superblock. Now a candidate for the ground state of the superblock, which is a reduced version of the full system, may be found. It may have a rather poor accuracy, but the method is iterative and improves with the steps below.
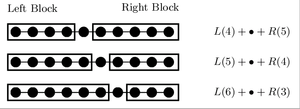The candidate ground state that has been found is projected into the subspace for each block using a density matrix
, whence the name. Thus, the relevant states for each block are updated.
Now one of the blocks grows at the expense of the other and the procedure is repeated. When the growing block reaches maximum size, the other starts to grow in its place. Each time we return to the original (equal sizes) situation, we say that a sweep has been completed. Normally, a few sweeps are enough to get a precision of a part in 1010 for a 1D lattice.
The first application of the DMRG, by Steven White and Reinhard Noack, was a toy model: to find the spectrum of a spin
0 particle in a 1D box. This model had been proposed by Kenneth G. Wilson
as a test for any new renormalization group
method, because they all happened to fail with this simple problem. The DMRG overcame the problems of previous renormalization group
methods by connecting two blocks with the two sites in the middle rather than just adding a single site to a block at each step as well as by using the density matrix
to identify the most important states to be kept at the end of each step. After succeeding with the toy model, the DMRG method was tried with success on the Heisenberg model (quantum)
.
in a transverse field, Heisenberg model
, etc., fermionic systems, such as the Hubbard model
, problems with impurities such as the Kondo effect
, boson
systems, and the physics of quantum dots joined with quantum wire
s. It has been also extended to work on tree graphs, and has found applications in the study of dendrimers. For 2D systems with one of the dimensions much larger than the other DMRG is also accurate, and has proved useful in the study of ladders.
The method has been extended to study equilibrium statistical physics
in 2D, and to analyze non-equilibrium phenomena in 1D.
The DMRG has also been applied to the field of Quantum Chemistry
to study strongly correlated systems.
where
are the values of the, e.g. z-component of the spin in a spin chain, and the Asi are matrices of arbitrary dimension m. As m → ∞, the representation becomes exact. This theory was exposed by S. Rommer and S. Ostlund in http://arxiv.org/abs/cond-mat/9606213.
method was developed to implement real time evolution of Matrix Product States. The idea is based on the classical simulation of a quantum computer
. Subsequently, a new method was devised to compute real time evolution within the DMRG formalism - See the paper by A. Feiguin and S.R. White http://arxiv.org/abs/cond-mat/0502475.
In recent years, some proposals to extend the method to 2D and 3D have been put forward, extending the definition of the Matrix Product States. See this paper by F. Verstraete and I. Cirac, http://arxiv.org/abs/cond-mat/0407066.
Quantum
In physics, a quantum is the minimum amount of any physical entity involved in an interaction. Behind this, one finds the fundamental notion that a physical property may be "quantized," referred to as "the hypothesis of quantization". This means that the magnitude can take on only certain discrete...
many-body systems with high accuracy. It was invented in 1992 by Steven R. White
Steven R. White
Steven R. White is the professor of physics at the University of California at Irvine. He graduated from University of California at San Diego; he then received his Ph.D. at Cornell University. He is most known for inventing the Density Matrix Renormalization Group in 1992...
and it is nowadays the most efficient method for 1-dimensional systems.
The idea behind DMRG
The main problem of quantumQuantum
In physics, a quantum is the minimum amount of any physical entity involved in an interaction. Behind this, one finds the fundamental notion that a physical property may be "quantized," referred to as "the hypothesis of quantization". This means that the magnitude can take on only certain discrete...
many-body physics is the fact that the Hilbert space grows exponentially with size. For example, a spin-1/2 chain of length L has 2 L degrees of freedom. The DMRG is an iterative, variational method that reduces effective degrees of freedom to those most important for a target state. The target state is often the ground state.
After a warmup cycle, the method splits the system into two blocks, which need not have equal sizes, and two sites in between. A set of representative states has been chosen for the block during the warmup. This set of left block + two sites + right block is known as the superblock. Now a candidate for the ground state of the superblock, which is a reduced version of the full system, may be found. It may have a rather poor accuracy, but the method is iterative and improves with the steps below.
Density matrix
In quantum mechanics, a density matrix is a self-adjoint positive-semidefinite matrix of trace one, that describes the statistical state of a quantum system...
, whence the name. Thus, the relevant states for each block are updated.
Now one of the blocks grows at the expense of the other and the procedure is repeated. When the growing block reaches maximum size, the other starts to grow in its place. Each time we return to the original (equal sizes) situation, we say that a sweep has been completed. Normally, a few sweeps are enough to get a precision of a part in 1010 for a 1D lattice.
Spin (physics)
In quantum mechanics and particle physics, spin is a fundamental characteristic property of elementary particles, composite particles , and atomic nuclei.It is worth noting that the intrinsic property of subatomic particles called spin and discussed in this article, is related in some small ways,...
0 particle in a 1D box. This model had been proposed by Kenneth G. Wilson
Kenneth G. Wilson
Kenneth Geddes Wilson is an American theoretical physicist and Nobel Prize winner.As an undergraduate at Harvard, he was a Putnam Fellow. He earned his PhD from Caltech in 1961, studying under Murray Gell-Mann....
as a test for any new renormalization group
Renormalization group
In theoretical physics, the renormalization group refers to a mathematical apparatus that allows systematic investigation of the changes of a physical system as viewed at different distance scales...
method, because they all happened to fail with this simple problem. The DMRG overcame the problems of previous renormalization group
Renormalization group
In theoretical physics, the renormalization group refers to a mathematical apparatus that allows systematic investigation of the changes of a physical system as viewed at different distance scales...
methods by connecting two blocks with the two sites in the middle rather than just adding a single site to a block at each step as well as by using the density matrix
Density matrix
In quantum mechanics, a density matrix is a self-adjoint positive-semidefinite matrix of trace one, that describes the statistical state of a quantum system...
to identify the most important states to be kept at the end of each step. After succeeding with the toy model, the DMRG method was tried with success on the Heisenberg model (quantum)
Heisenberg model (quantum)
The Heisenberg model is a statistical mechanical model used in the study of critical points and phase transitions of magnetic systems, in which the spin of the magnetic systems are treated quantum mechanically...
.
Technical details about the implementation
A practical implementation of the DMRG algorithm is a lengthy work. A few of the main computational tricks are these:- The ground state for the superblock is obtained using the Lanczos algorithmLanczos algorithmThe Lanczos algorithm is an iterative algorithm invented by Cornelius Lanczos that is an adaptation of power methods to find eigenvalues and eigenvectors of a square matrix or the singular value decomposition of a rectangular matrix. It is particularly useful for finding decompositions of very...
of matrix diagonalization. Another choice is the Arnoldi methodArnoldi iterationIn numerical linear algebra, the Arnoldi iteration is an eigenvalue algorithm and an important example of iterative methods. Arnoldi finds the eigenvalues of general matrices; an analogous method for Hermitian matrices is the Lanczos iteration. The Arnoldi iteration was invented by W. E...
, especially when dealing with non-hermitian matrices.
- The Lanczos algorithm usually starts with a random seed. In DMRG, the ground state obtained in a certain DMRG step, suitably transformed, may serve as a better seed for the Lanczos algorithm at the next DMRG step.
- In systems with symmetries, we may have conserved quantum numbers, such as total spin in a Heisenberg model (quantum)Heisenberg model (quantum)The Heisenberg model is a statistical mechanical model used in the study of critical points and phase transitions of magnetic systems, in which the spin of the magnetic systems are treated quantum mechanically...
. It is convenient to find the ground state within each of the sectors into which the Hilbert space is divided.
- An example: dmrg of Heisenberg modelDmrg of Heisenberg modelThis example presents the infinite DMRG algorithm. It is about S=1 antiferromagnetic Heisenberg chain, but the recipe can be applied for every translationally invariant one-dimensional lattice...
Applications
The DMRG has been successfully applied to get the low energy properties of spin chains: Ising modelIsing model
The Ising model is a mathematical model of ferromagnetism in statistical mechanics. The model consists of discrete variables called spins that can be in one of two states . The spins are arranged in a graph , and each spin interacts with its nearest neighbors...
in a transverse field, Heisenberg model
Heisenberg model
The Heisenberg model can refer to two models in statistical mechanics:*Heisenberg model , a classical nearest neighbour spin model*Heisenberg model , a model where the spins are treated quantum mechanically using Pauli matrices....
, etc., fermionic systems, such as the Hubbard model
Hubbard model
The Hubbard model is an approximate model used, especially in solid state physics, to describe the transition between conducting and insulating systems...
, problems with impurities such as the Kondo effect
Kondo effect
In physics, the Kondo effect describes the scattering of conduction electrons in a metal due to magnetic impurities. It is a measure of how electrical resistivity changes with temperature....
, boson
Boson
In particle physics, bosons are subatomic particles that obey Bose–Einstein statistics. Several bosons can occupy the same quantum state. The word boson derives from the name of Satyendra Nath Bose....
systems, and the physics of quantum dots joined with quantum wire
Quantum wire
In condensed matter physics, a quantum wire is an electrically conducting wire, in which quantum effects are affecting transport properties. Due to the quantum confinement of conduction electrons in the transverse direction of the wire, their transverse energy is quantized into a series of...
s. It has been also extended to work on tree graphs, and has found applications in the study of dendrimers. For 2D systems with one of the dimensions much larger than the other DMRG is also accurate, and has proved useful in the study of ladders.
The method has been extended to study equilibrium statistical physics
Statistical physics
Statistical physics is the branch of physics that uses methods of probability theory and statistics, and particularly the mathematical tools for dealing with large populations and approximations, in solving physical problems. It can describe a wide variety of fields with an inherently stochastic...
in 2D, and to analyze non-equilibrium phenomena in 1D.
The DMRG has also been applied to the field of Quantum Chemistry
Quantum chemistry
Quantum chemistry is a branch of chemistry whose primary focus is the application of quantum mechanics in physical models and experiments of chemical systems...
to study strongly correlated systems.
The matrix product ansatz
The success of the DMRG for 1D systems is related to the fact that it is a variational method within the space of matrix product states. These are states of the form
where
are the values of the, e.g. z-component of the spin in a spin chain, and the Asi are matrices of arbitrary dimension m. As m → ∞, the representation becomes exact. This theory was exposed by S. Rommer and S. Ostlund in http://arxiv.org/abs/cond-mat/9606213.Extensions of DMRG
In 2004 the time-evolving block decimationTime-evolving block decimation
The time-evolving block decimation algorithm is a numerical scheme used to simulate one-dimensional quantum many-body systems, characterized by at most nearest-neighbour interactions....
method was developed to implement real time evolution of Matrix Product States. The idea is based on the classical simulation of a quantum computer
Quantum computer
A quantum computer is a device for computation that makes direct use of quantum mechanical phenomena, such as superposition and entanglement, to perform operations on data. Quantum computers are different from traditional computers based on transistors...
. Subsequently, a new method was devised to compute real time evolution within the DMRG formalism - See the paper by A. Feiguin and S.R. White http://arxiv.org/abs/cond-mat/0502475.
In recent years, some proposals to extend the method to 2D and 3D have been put forward, extending the definition of the Matrix Product States. See this paper by F. Verstraete and I. Cirac, http://arxiv.org/abs/cond-mat/0407066.
Further reading
- The original paper, by S. R. White, http://prola.aps.org/abstract/PRL/v69/i19/p2863_1 or http://hedrock.ps.uci.edu/dmrgpaper/dmrgpap.pdf
- A broad review, by Karen Hallberg, http://arxiv.org/abs/cond-mat/0609039.
- Two reviews by Ulrich Schollwöck, one discussing the original formulation http://arxiv.org/abs/cond-mat/0409292, and another in terms of matrix product states http://arxiv.org/abs/1008.3477
- The Ph.D. thesis of Javier Rodríguez Laguna http://arxiv.org/abs/cond-mat/0207340.
- An introduction to DMRG and its time-dependent extension http://arxiv.org/abs/cond-mat/0603842.
- A list of DMRG e-prints on arxiv.org http://quattro.phys.sci.kobe-u.ac.jp/dmrg/condmat.html.
Related software
- Powder with Power: a free distribution of time-dependent DMRG code written in FortranFortranFortran is a general-purpose, procedural, imperative programming language that is especially suited to numeric computation and scientific computing...
http://www.dmrg.it - The ALPS Project: a free distribution of time-independent DMRG code and Quantum Monte CarloQuantum Monte CarloQuantum Monte Carlo is a large class of computer algorithms that simulate quantum systems with the idea of solving the quantum many-body problem. They use, in one way or another, the Monte Carlo method to handle the many-dimensional integrals that arise...
codes written in C++C++C++ is a statically typed, free-form, multi-paradigm, compiled, general-purpose programming language. It is regarded as an intermediate-level language, as it comprises a combination of both high-level and low-level language features. It was developed by Bjarne Stroustrup starting in 1979 at Bell...
http://alps.comp-phys.org
See also
- Quantum Monte CarloQuantum Monte CarloQuantum Monte Carlo is a large class of computer algorithms that simulate quantum systems with the idea of solving the quantum many-body problem. They use, in one way or another, the Monte Carlo method to handle the many-dimensional integrals that arise...
- Dmrg of Heisenberg modelDmrg of Heisenberg modelThis example presents the infinite DMRG algorithm. It is about S=1 antiferromagnetic Heisenberg chain, but the recipe can be applied for every translationally invariant one-dimensional lattice...
- Time-evolving block decimationTime-evolving block decimationThe time-evolving block decimation algorithm is a numerical scheme used to simulate one-dimensional quantum many-body systems, characterized by at most nearest-neighbour interactions....
- Configuration interactionConfiguration interactionConfiguration interaction is a post-Hartree–Fock linear variational method for solving the nonrelativistic Schrödinger equation within the Born–Oppenheimer approximation for a quantum chemical multi-electron system. Mathematically, configuration simply describes the linear combination...