In geometry

Geometry

Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....

, the deltoidal trihexagonal tiling is a dual of the semiregular tiling.

Conway

John Horton Conway

John Horton Conway is a prolific mathematician active in the theory of finite groups, knot theory, number theory, combinatorial game theory and coding theory...

 calls it a tetrille.

The edges of this tiling can be formed by the intersection overlay of the regular triangular tiling and a hexagonal tiling.

Dual tiling

The deltoidal trihexagonal tiling is a dual of the semiregular tiling rhombitrihexagonal tiling. Its faces are deltoids or kites

Kite (geometry)

In Euclidean geometry a kite is a quadrilateral whose four sides can be grouped into two pairs of equal-length sides that are next to each other. In contrast, a parallelogram also has two pairs of equal-length sides, but they are opposite each other rather than next to each other...

.

Topological relations

This tiling is related to the trihexagonal tiling

Trihexagonal tiling

In geometry, the trihexagonal tiling is a semiregular tiling of the Euclidean plane. There are two triangles and two hexagons alternating on each vertex...

 by dividing the triangles and hexagons into central triangles and merging neighboring triangles into kites.

This tiling is topologically related to three catalan solid

Catalan solid

In mathematics, a Catalan solid, or Archimedean dual, is a dual polyhedron to an Archimedean solid. The Catalan solids are named for the Belgian mathematician, Eugène Catalan, who first described them in 1865....

s, with face configuration

Face configuration

In geometry, a face configuration is notational description of a face-transitive polyhedron. It represents a sequential count of the number of faces that exist at each vertex around a face....

s 3.4.n.4, and continues into tilings of the hyperbolic plane

Hyperbolic space

In mathematics, hyperbolic space is a type of non-Euclidean geometry. Whereas spherical geometry has a constant positive curvature, hyperbolic geometry has a negative curvature: every point in hyperbolic space is a saddle point...

. These face-transitive figures have (*n32) reflectional symmetry.

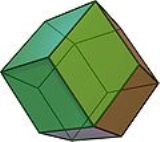
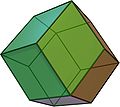V3.4.3.4 Rhombic dodecahedron In geometry, the rhombic dodecahedron is a convex polyhedron with 12 rhombic faces. It is an Archimedean dual solid, or a Catalan solid. Its dual is the cuboctahedron.-Properties:... (*332) and (*432)

V3.4.4.4 Deltoidal icositetrahedron In geometry, a deltoidal icositetrahedron is a Catalan solid which looks a bit like an overinflated cube. Its dual polyhedron is the rhombicuboctahedron.... (*432)

V3.4.5.4 Deltoidal hexecontahedron In geometry, a deltoidal hexecontahedron is a catalan solid which looks a bit like an overinflated dodecahedron. It is sometimes also called the trapezoidal hexecontahedron or strombic hexecontahedron... (*532)

V3.4.6.4 (*632)

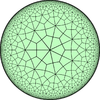V3.4.7.4 (*732)