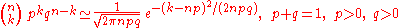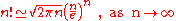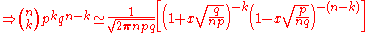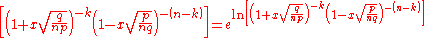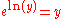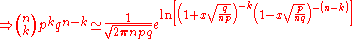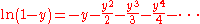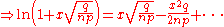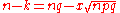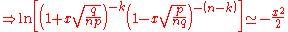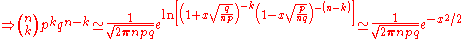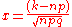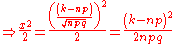In probability theory

Probability theory

Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...

, the de Moivre–Laplace theorem is a normal approximation to the binomial distribution. It is a special case of the central limit theorem

Central limit theorem

In probability theory, the central limit theorem states conditions under which the mean of a sufficiently large number of independent random variables, each with finite mean and variance, will be approximately normally distributed. The central limit theorem has a number of variants. In its common...

. It states that the binomial distribution of the number of "successes" in n independent

Statistical independence

In probability theory, to say that two events are independent intuitively means that the occurrence of one event makes it neither more nor less probable that the other occurs...

 Bernoulli trial

Bernoulli trial

In the theory of probability and statistics, a Bernoulli trial is an experiment whose outcome is random and can be either of two possible outcomes, "success" and "failure"....

s with probability p of success on each trial is approximately a normal distribution with mean np and standard deviation , if n is very large and some conditions are satisfied.

The theorem appeared in the second edition of The Doctrine of Chances

The Doctrine of Chances

The Doctrine of Chances was the first textbook on probability theory, written by 18th-century French mathematician Abraham de Moivre and first published in 1718. De Moivre wrote in English because he resided in England at the time, having fled France to escape the persecution of Huguenots...

by Abraham de Moivre

Abraham de Moivre

Abraham de Moivre was a French mathematician famous for de Moivre's formula, which links complex numbers and trigonometry, and for his work on the normal distribution and probability theory. He was a friend of Isaac Newton, Edmund Halley, and James Stirling...

, published in 1738. The "Bernoulli trials" were not so-called in that book, but rather de Moivre wrote about the probability distribution

Probability distribution

In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....

 of the number of times "heads" appears when a coin is tossed 3600 times.

Theorem

As n grows large, for k in the neighborhood of np we can approximate

in the sense that the ratio of the left-hand side to the right-hand side converges to 1 as .

Proof

According to Stirling's formula, we can replace the factorial of a large number n, with the approximation:

or:

Thus

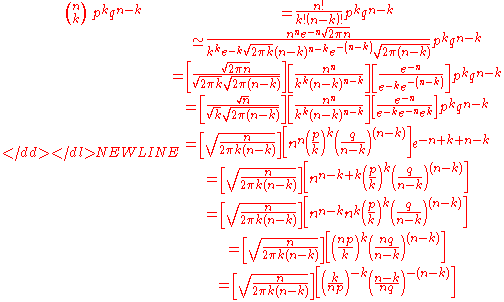
Now, let

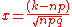
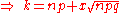 and 

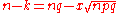
  and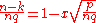 

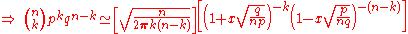
Now, consider the first square bracket term.

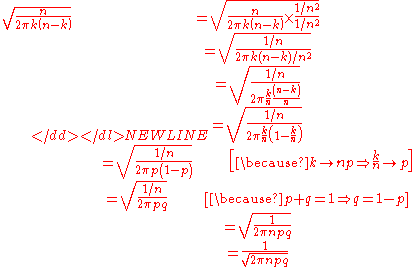
Now, consider the term in the second square bracket.

The above conversion is based on the fact that the natural logarithm function, if considered as a real-valued function of a real variable, is the inverse function of the exponential function, leading to the identity given below:

Now, consider the natural logarithm term.

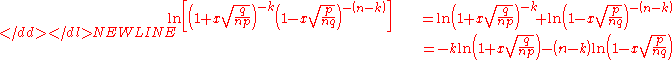
Now, using the following two series we will solve the above natural logarithm:-

and

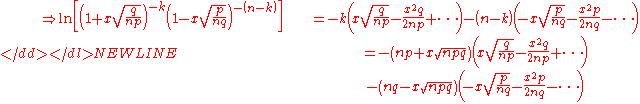
because

and so

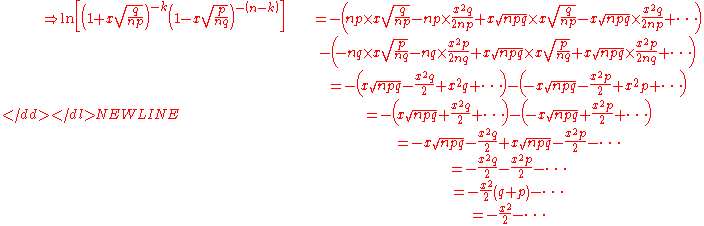
We can ignore the terms where the power of x is greater than 3 in the above expansion, since x approaches 0 as n gets large, because x is proportional to , and → .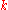



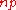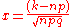
Now,

Thus,

and the result is proved.

The source of this article is wikipedia, the free encyclopedia.  The text of this article is licensed under the GFDL.