De Moivre's law
Encyclopedia
De Moivre's Law is a survival model applied in actuarial science
, named for Abraham de Moivre
. It is a simple law of mortality based on a linear survival function
.
parameter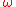
called the ultimate age. Under de Moivre's
law, a newborn has probability of surviving at least x years given by the
survival function
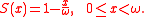
Under this model, the conditional probability that a life aged x years survives
at least t years is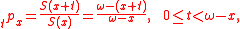
and the future lifetime random variable T(x) therefore follows a uniform distribution
on
.
The force of mortality
(hazard rate or failure rate
) for a life aged x is
which has the property of increasing failure rate (IFR) with respect to age that is usually assumed for humans, or anything subject to aging.
De Moivre's law is applied as a simple analytical law of mortality and the linear assumption is also applied as a model for interpolation for discrete survival models such as life table
s.
. If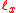
denotes the number of survivors at exact age x years out of an initial cohort of 
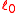lives, the UDD assumption for fractional years is that
or equivalently, that
Under the UDD assumption, the probability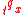
that a life aged x fails within (0,t), is 
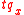, and 
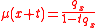, for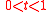 
.
Actuarial science
Actuarial science is the discipline that applies mathematical and statistical methods to assess risk in the insurance and finance industries. Actuaries are professionals who are qualified in this field through education and experience...
, named for Abraham de Moivre
Abraham de Moivre
Abraham de Moivre was a French mathematician famous for de Moivre's formula, which links complex numbers and trigonometry, and for his work on the normal distribution and probability theory. He was a friend of Isaac Newton, Edmund Halley, and James Stirling...
. It is a simple law of mortality based on a linear survival function
Survival function
The survival function, also known as a survivor function or reliability function, is a property of any random variable that maps a set of events, usually associated with mortality or failure of some system, onto time. It captures the probability that the system will survive beyond a specified time...
.
Definition
De Moivre's law has a singleparameter
called the ultimate age. Under de Moivre'slaw, a newborn has probability of surviving at least x years given by the
survival function
Survival function
The survival function, also known as a survivor function or reliability function, is a property of any random variable that maps a set of events, usually associated with mortality or failure of some system, onto time. It captures the probability that the system will survive beyond a specified time...
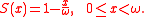
Under this model, the conditional probability that a life aged x years survives
at least t years is
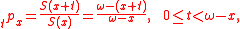
and the future lifetime random variable T(x) therefore follows a uniform distribution
Uniform distribution (continuous)
In probability theory and statistics, the continuous uniform distribution or rectangular distribution is a family of probability distributions such that for each member of the family, all intervals of the same length on the distribution's support are equally probable. The support is defined by...
on
.The force of mortality
Force of mortality
In actuarial science, force of mortality represents the instantaneous rate of mortality at a certain age measured on an annualized basis. It is identical in concept to failure rate, also called hazard function, in reliability theory....
(hazard rate or failure rate
Failure rate
Failure rate is the frequency with which an engineered system or component fails, expressed for example in failures per hour. It is often denoted by the Greek letter λ and is important in reliability engineering....
) for a life aged x is
which has the property of increasing failure rate (IFR) with respect to age that is usually assumed for humans, or anything subject to aging.
De Moivre's law is applied as a simple analytical law of mortality and the linear assumption is also applied as a model for interpolation for discrete survival models such as life table
Life table
In actuarial science, a life table is a table which shows, for each age, what the probability is that a person of that age will die before his or her next birthday...
s.
Linear assumption for fractional years
When applied for interpolation, the linear assumption is called uniform distribution of death (UDD) assumption in fractional years and it is equivalent to linear interpolationLinear interpolation
Linear interpolation is a method of curve fitting using linear polynomials. Lerp is an abbreviation for linear interpolation, which can also be used as a verb .-Linear interpolation between two known points:...
. If
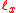denotes the number of survivors at exact age x years out of an initial cohort of 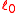lives, the UDD assumption for fractional years is thator equivalently, that
Under the UDD assumption, the probability
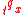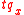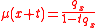that a life aged x fails within (0,t), is , and , for 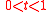.