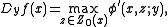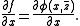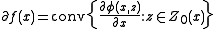Danskin's theorem
Encyclopedia
In convex analysis
, Danskin's theorem is a theorem
which provides information about the derivative
s of a function
of the form
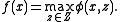
The theorem has applications in optimization
, where it sometimes is used to solve minimax
problems.
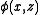 is a continuous function
is a continuous function
of two arguments,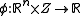
where is a compact set. Further assume that
is a compact set. Further assume that 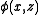 is convex
is convex
in for every
for every 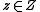 .
.
Under these conditions, Danskin's theorem provides conclusions regarding the differentiability of the function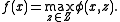
To state these results, we define the set of maximizing points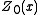 as
as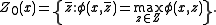
Danskin's theorem then provides the following results.
Convexity
Directional derivatives
Derivative
Subdifferential
Convex analysis
Convex analysis is the branch of mathematics devoted to the study of properties of convex functions and convex sets, often with applications in convex minimization, a subdomain of optimization theory....
, Danskin's theorem is a theorem
Theorem
In mathematics, a theorem is a statement that has been proven on the basis of previously established statements, such as other theorems, and previously accepted statements, such as axioms...
which provides information about the derivative
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
s of a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
of the form
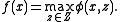
The theorem has applications in optimization
Optimization (mathematics)
In mathematics, computational science, or management science, mathematical optimization refers to the selection of a best element from some set of available alternatives....
, where it sometimes is used to solve minimax
Minimax
Minimax is a decision rule used in decision theory, game theory, statistics and philosophy for minimizing the possible loss for a worst case scenario. Alternatively, it can be thought of as maximizing the minimum gain...
problems.
Statement
The theorem applies to the following situation. Suppose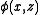 is a continuous function
is a continuous functionContinuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
of two arguments,
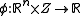
where
 is a compact set. Further assume that
is a compact set. Further assume that 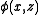 is convex
is convexConvex function
In mathematics, a real-valued function f defined on an interval is called convex if the graph of the function lies below the line segment joining any two points of the graph. Equivalently, a function is convex if its epigraph is a convex set...
in
 for every
for every 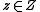 .
.Under these conditions, Danskin's theorem provides conclusions regarding the differentiability of the function
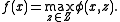
To state these results, we define the set of maximizing points
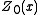 as
as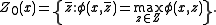
Danskin's theorem then provides the following results.
Convexity
-
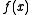 is convexConvex functionIn mathematics, a real-valued function f defined on an interval is called convex if the graph of the function lies below the line segment joining any two points of the graph. Equivalently, a function is convex if its epigraph is a convex set...
is convexConvex functionIn mathematics, a real-valued function f defined on an interval is called convex if the graph of the function lies below the line segment joining any two points of the graph. Equivalently, a function is convex if its epigraph is a convex set...
.
Directional derivatives
- The directional derivativeDirectional derivativeIn mathematics, the directional derivative of a multivariate differentiable function along a given vector V at a given point P intuitively represents the instantaneous rate of change of the function, moving through P in the direction of V...
of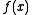 in the direction
in the direction  , denoted
, denoted 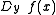 , is given by
, is given by
- where
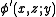 is the directional derivative of the function
is the directional derivative of the function 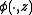 at
at  in the direction
in the direction 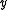 .
.
Derivative
-
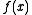 is differentiable at
is differentiable at  if
if 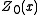 consists of a single element
consists of a single element 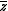 . In this case, the derivativeDerivativeIn calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
. In this case, the derivativeDerivativeIn calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
of (or the gradientGradientIn vector calculus, the gradient of a scalar field is a vector field that points in the direction of the greatest rate of increase of the scalar field, and whose magnitude is the greatest rate of change....
(or the gradientGradientIn vector calculus, the gradient of a scalar field is a vector field that points in the direction of the greatest rate of increase of the scalar field, and whose magnitude is the greatest rate of change....
of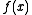 if
if  is a vector) is given by
is a vector) is given by
-
Subdifferential
- If
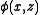 is differentiable with respect to
is differentiable with respect to  for all
for all 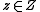 , and if
, and if 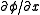 is continuous with respect to
is continuous with respect to  for all
for all  , then the subdifferential of
, then the subdifferential of 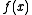 is given by
is given by
-
- where
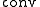 indicates the convex hullConvex hullIn mathematics, the convex hull or convex envelope for a set of points X in a real vector space V is the minimal convex set containing X....
indicates the convex hullConvex hullIn mathematics, the convex hull or convex envelope for a set of points X in a real vector space V is the minimal convex set containing X....
operation.