
Dadda multiplier
Encyclopedia


Luigi Dadda
Luigi Dadda is an Italian computer engineer. He was born on April 29, 1923 in Lodi. He was among the first researchers on computers in Italy. He has been a rector of the Politecnico di Milano technical university for 12 years, and he still performs research in the same university.He studied...
in 1965. It is similar to the Wallace multiplier, but it is slightly faster (for all operand sizes) and requires fewer gates (for all but the smallest operand sizes).http://www.cerc.utexas.edu/~whitney/pdfs/spie03.pdf
In fact, Dadda and Wallace multipliers have the same 3 steps:
- Multiply (that is - AND) each bit of one of the arguments, by each bit of the other, yielding
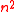 results. Depending on position of the multiplied bits, the wires carry different weights, for example wire of bit carrying result of
results. Depending on position of the multiplied bits, the wires carry different weights, for example wire of bit carrying result of 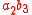 is 32.
is 32. - Reduce the number of partial products to two layers of full and half adders.
- Group the wires in two numbers, and add them with a conventional adderAdder (electronics)In electronics, an adder or summer is a digital circuit that performs addition of numbers.In many computers and other kinds of processors, adders are used not only in the arithmetic logic unit, but also in other parts of the processor, where they are used to calculate addresses, table indices, and...
.
However, unlike Wallace multipliers that reduce as much as
possible on each layer, Dadda multipliers do as few reductions as
possible. Because of this, Dadda multipliers have less expensive
reduction phase, but the numbers may be a few bits longer, thus
requiring slightly bigger adders.
To achieve this, the structure of the second step is governed by
slightly more complex rules than in the Wallace tree. As in the
Wallace tree, a new layer is added if any weight is carried by 3
or more wires. The reduction rules however are as follows:
- Take any 3 wires with the same weights and input them into a full adder. The result will be an output wire of the same weight and an output wire with a higher weight for each 3 input wires.
- If there are 2 wires of the same weight left, and the current number of output wires with that weight is equal to 2 (modulo 3), input them into a half adder. Otherwise, pass them through to the next layer.
- If there is just 1 wire left, connect it to the next layer.
This step does only as many adds as necessary, so that the number
of output weights stays close to a multiple of 3, which is the
ideal number of weights when using full adders as 3:2 compressors.
However, when a layer carries at most 3 input wires for any
weight, that layer will be the last one. In this case, the Dadda
tree will use half adder more aggressively (but still not as much
as in a Wallace multiplier), to ensure that there are only two
outputs for any weight. Then, the second rule above changes as
follows:
- If there are 2 wires of the same weight left, and the current number of output wires with that weight is equal to 1 or 2 (modulo 3), input them into a half adder. Otherwise, pass them through to the next layer.
Algorithm example
This section explains the Dadda dot-diagram reduction example- Let d1 = 2 and dj+1 = floor(3*dj/2)
- This generates the sequence: d1=2, d2=3, d3=4, ...
- Find the largest dj that is less than the maximum number of bits in any column.
- For our example to the right, this would be 6
- For every column, use full adders (FA) and half adders (HA) to ensure that the number of elements in each column will be <= nj
- When doing this, keep in mind that any column n that has an adder within it, will pass its sum bit to the next stage in column n and the carry bit to the n+1 column. The n+1 column will need to take this into account when determining the number of adders to use.
First bank
- Columns 0-5 don't need any adders since they all have <= 6 bits
- Column 6 needs 1 HA (7 > 6) which reduces it to 6 bits and passes one carry bit to column 7.
- Column 7 can use a FA since it has 8 bits which would reduce the column to 6 bits, but since column 6 is passing in a carry bit, it needs one more HA to bring the total to 6 bits
- Column 8 needs a FA and a HA since it's getting 2 carry bits from column 7's adders.
- Column 9 only needs one FA
- Columns 10-14 do not need any adders since any carry bits from the previous columns don't result in a total greater than 6.
Second bank
- The next bank's dj = 4
- Columns 0-3 don't need any adders since they have <=4 bits
- Column 4 needs a HA, (5 > 4)
- Column 5 needs a FA and a HA due to the carry bit
- Columns 6-10 need two FA since they all have 2 carry bits coming from the previous stage
- Column 11 only needs 1 FA to get to 4 bits after the carry bits come in
- Columns 12-14 don't need any adders since they all have < 4 bits
3rd bank
- The next bank's dj = 3
- Columns 0-2 don't need any adders since they have <=3 bits
- Column 3 only needs one HA to get to 3 bits
- Column 4-12 need a FA since they all have one carry-in bit coming in from the previous column
- Columns 13-14 don't need any adders since they have < 3 bits
4th bank
- The next bank's dj = 2
- Columns 0-1 don't need any adders since they have <=2 bits
- Column 2 only needs one HA to get to 2 bits
- Column 3-13 need a FA since they all have one carry-in bit coming in from the previous column
- Column 14 doesn't need an adder (1 < 2)
5th bank
- At this point, everything is reduced to two bits and the resultant can be calculated from a 14 bit adder.
Example
 , multiplying
, multiplying 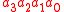 by
by 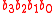 :
:- Reduction layer 1:
- Pass the only weight-1 wire through, output: 1 weight-1 wire
- Pass the two weight-2 wires through, outputs: 2 weight-2 wires
- Add a full adder for weight 4, outputs: 1 weight-4 wire, 1 weight-8 wire
- Add a full adder for weight 8, and pass the remaining wire through, outputs: 2 weight-8 wires, 1 weight-16 wire
- Add a full adder for weight 16, outputs: 1 weight-16 wire, 1 weight-32 wire
- Pass the two weight-32 wires through, outputs: 2 weight-32 wires
- Pass the only weight-64 wire through, output: 1 weight-64 wire
- Wires at the output of reduction layer 1:
- weight 1 - 1
- weight 2 - 2
- weight 4 - 1
- weight 8 - 3
- weight 16 - 2
- weight 32 - 3
- weight 64 - 1
- Reduction layer 2: this layer will be the last because any weight has at most three input wires.
- Weights 1, 2, 4, 64 pass through.
- Add a full adder for weight 8, outputs: 1 weight-8 wire, 1 weight-16 wire
- Add a half adder for weight 16, outputs: 1 weight-16 wire, 1 weight-32 wire
Weight 8's full adder has already produced one weight-16 output wire. By using a half adder for the two weight-16 input wires, the Dadda's tree ensures that the last layer has only two output wires for any weight. - Add a full adder for weight 32, outputs: 1 weight-32 wire, 1 weight-64 wire
- Outputs:
- weight 1 - 1
- weight 2 - 2
- weight 4 - 1
- weight 8 - 1
- weight 16 - 2
- weight 32 - 2
- weight 64 - 2
Compared to a Wallace tree, which requires 10 between full adders
and half adders, the reduction phase of the Dadda multiplier has
the same delay but requires only six. On the other hand, the
final adder has 6-bit inputs (weights 2 to 64), rather than
5-bit (weights 8 to 128) as in Wallace tree......
See also
- Booth's multiplication algorithmBooth's multiplication algorithmBooth's multiplication algorithm is a multiplication algorithm that multiplies two signed binary numbers in two's complement notation. The algorithm was invented by Andrew Donald Booth in 1950 while doing research on crystallography at Birkbeck College in Bloomsbury, London...
- Fused multiply–add
- Wallace treeWallace treeA Wallace tree is an efficient hardware implementation of a digital circuit that multiplies two integers, devised by an Australian Computer Scientist Chris Wallace in 1964.The Wallace tree has three steps:...
- BKM algorithmBKM algorithmThe BKM algorithm is a shift-and-add algorithm for computing elementary functions, first published in 1994 by J.C. Bajard, S. Kla, and J.M. Muller. BKM is based on computing complex logarithms and exponentials using a method similar to the algorithm Henry Briggs used to compute logarithms...
for complex logarithms and exponentials - Kochanski multiplicationKochanski multiplicationKochanski multiplication is an algorithm that allows modular arithmetic to be performed efficiently when the modulus is large...
for modularModular arithmeticIn mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
multiplication

