
Cutler's bar notation
Encyclopedia
In mathematics
, Cutler's bar notation is a notation system for large numbers, introduced by Mark Cutler in 2004. The idea is based on iterated exponentiation in much the same way that exponentiation
is iterated
multiplication
.
can be expressed as such:

However, these expressions become arbitrarily large when dealing with systems such as Knuth's up-arrow notation
. Take the following:
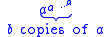
Cutler's bar notation shifts these exponentials counterclockwise, forming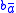 . A bar is placed above the variable to denote this change. As such:
. A bar is placed above the variable to denote this change. As such:
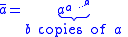
This system becomes effective with multiple exponent, when regular denotation becomes too cumbersome.
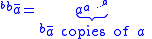
At any time, this can be further shortened by rotating the exponential counter-clockwise once more.
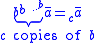
The same pattern could be iterated a fourth time, becoming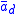 . For this reason, it is sometimes referred to as Cutler's circular notation.
. For this reason, it is sometimes referred to as Cutler's circular notation.
 would contain more than a googolplex digits, whilst remaining fairly simple to write with and remember.
would contain more than a googolplex digits, whilst remaining fairly simple to write with and remember.
However, the system reaches a problem when dealing with different exponents in a single expression. For instance, the expression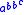 could not be summarised in Bar notation. Additionally, the exponent can only be shifted thrice before it returns to its original position, making a five degree shift indistinguishable from a one degree shift. Some have suggested using a double and triple bar in subsequent rotations, though this presents problems when dealing with ten and twenty degree shifts.
could not be summarised in Bar notation. Additionally, the exponent can only be shifted thrice before it returns to its original position, making a five degree shift indistinguishable from a one degree shift. Some have suggested using a double and triple bar in subsequent rotations, though this presents problems when dealing with ten and twenty degree shifts.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Cutler's bar notation is a notation system for large numbers, introduced by Mark Cutler in 2004. The idea is based on iterated exponentiation in much the same way that exponentiation
Exponentiation
Exponentiation is a mathematical operation, written as an, involving two numbers, the base a and the exponent n...
is iterated
Iteration
Iteration means the act of repeating a process usually with the aim of approaching a desired goal or target or result. Each repetition of the process is also called an "iteration," and the results of one iteration are used as the starting point for the next iteration.-Mathematics:Iteration in...
multiplication
Multiplication
Multiplication is the mathematical operation of scaling one number by another. It is one of the four basic operations in elementary arithmetic ....
.
Introduction
A regular exponentialExponentiation
Exponentiation is a mathematical operation, written as an, involving two numbers, the base a and the exponent n...
can be expressed as such:

However, these expressions become arbitrarily large when dealing with systems such as Knuth's up-arrow notation
Knuth's up-arrow notation
In mathematics, Knuth's up-arrow notation is a method of notation for very large integers, introduced by Donald Knuth in 1976. It is closely related to the Ackermann function and especially to the hyperoperation sequence. The idea is based on the fact that multiplication can be viewed as iterated...
. Take the following:
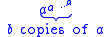
Cutler's bar notation shifts these exponentials counterclockwise, forming
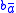 . A bar is placed above the variable to denote this change. As such:
. A bar is placed above the variable to denote this change. As such: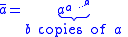
This system becomes effective with multiple exponent, when regular denotation becomes too cumbersome.
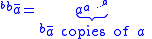
At any time, this can be further shortened by rotating the exponential counter-clockwise once more.
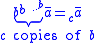
The same pattern could be iterated a fourth time, becoming
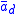 . For this reason, it is sometimes referred to as Cutler's circular notation.
. For this reason, it is sometimes referred to as Cutler's circular notation.Advantages and drawbacks
The Cutler Bar Notation can be used to easily express other notation systems in exponent form. It also allows for a flexible summarisation of multiple copies of the same exponents, where any number of stacked exponents can be shfted counter-clockwise and shortened to a single variable. The Bar Notation also allows for farily rapid composure of very large numbers. For instance, the number would contain more than a googolplex digits, whilst remaining fairly simple to write with and remember.
would contain more than a googolplex digits, whilst remaining fairly simple to write with and remember.However, the system reaches a problem when dealing with different exponents in a single expression. For instance, the expression
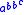 could not be summarised in Bar notation. Additionally, the exponent can only be shifted thrice before it returns to its original position, making a five degree shift indistinguishable from a one degree shift. Some have suggested using a double and triple bar in subsequent rotations, though this presents problems when dealing with ten and twenty degree shifts.
could not be summarised in Bar notation. Additionally, the exponent can only be shifted thrice before it returns to its original position, making a five degree shift indistinguishable from a one degree shift. Some have suggested using a double and triple bar in subsequent rotations, though this presents problems when dealing with ten and twenty degree shifts.

