
Current algebra
Encyclopedia
Current algebra is a mathematical framework in quantum field theory
where the fields form a Lie algebra
under their commutation relations.
For instance, in a non-Abelian
Yang–Mills
symmetry, where ρ is the charge density,
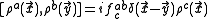
where f are the structure constants of the Lie algebra. If space is a one dimensional circle, there may exist central extensions.
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
where the fields form a Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
under their commutation relations.
For instance, in a non-Abelian
Non-abelian
In theoretical physics, a non-abelian gauge transformation means a gauge transformation taking values in some group G, the elements of which do not obey the commutative law when they are multiplied. The original choice of G in the physics of electromagnetism was U, which is commutative.For a...
Yang–Mills
Yang–Mills
Yang–Mills theory is a gauge theory based on the SU group. Wolfgang Pauli formulated in 1953 the first consistent generalization of the five-dimensional theory of Kaluza, Klein, Fock and others to a higher dimensional internal space...
symmetry, where ρ is the charge density,
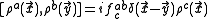
where f are the structure constants of the Lie algebra. If space is a one dimensional circle, there may exist central extensions.

