
Cramér's conjecture
Encyclopedia
In number theory
, Cramér's conjecture, formulated by the Swedish
mathematician
Harald Cramér
in 1936, states that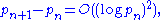
where pn denotes the nth prime number
, O is big O notation
, and "log" is the natural logarithm
. Intuitively, this means the gaps between consecutive primes are always small, and it quantifies asymptotically just how small they can be. This conjecture
has not been proven or disproven.
model (essentially a heuristic
) of the primes, in which one assumes that the probability that a natural number
x is prime is 1/log x. This is known as the Cramér model of the primes.
Cramér proved that in this model, the above conjecture holds true with probability one.
that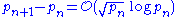
on the assumption of the Riemann hypothesis
.
In the other direction, E. Westzynthius proved in 1931 that prime gaps grow more than logarithmically. That is,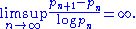
conjectured asymptotic equality of record gaps, a somewhat stronger statement than Cramér's conjecture.
In the random model, with
with 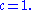
But this constant, , may not apply to all the primes, by Maier's theorem
, may not apply to all the primes, by Maier's theorem
. Andrew Granville
in 1995 proposed the constant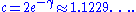
Thomas Nicely has calculated many large prime gaps. He measures the quality of fit to Cramér's conjecture by measuring the ratio R of the logarithm of a prime to the square root of the gap; he writes, “For the largest known maximal gaps, R has remained near 1.13,” showing that, at least within the range of his calculation, the Granville refinement of Cramér's conjecture seems to be a good fit to the data.
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, Cramér's conjecture, formulated by the Swedish
Sweden
Sweden , officially the Kingdom of Sweden , is a Nordic country on the Scandinavian Peninsula in Northern Europe. Sweden borders with Norway and Finland and is connected to Denmark by a bridge-tunnel across the Öresund....
mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
Harald Cramér
Harald Cramér
Harald Cramér was a Swedish mathematician, actuary, and statistician, specializing in mathematical statistics and probabilistic number theory. He was once described by John Kingman as "one of the giants of statistical theory".-Early life:Harald Cramér was born in Stockholm, Sweden on September...
in 1936, states that
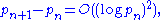
where pn denotes the nth prime number
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
, O is big O notation
Big O notation
In mathematics, big O notation is used to describe the limiting behavior of a function when the argument tends towards a particular value or infinity, usually in terms of simpler functions. It is a member of a larger family of notations that is called Landau notation, Bachmann-Landau notation, or...
, and "log" is the natural logarithm
Natural logarithm
The natural logarithm is the logarithm to the base e, where e is an irrational and transcendental constant approximately equal to 2.718281828...
. Intuitively, this means the gaps between consecutive primes are always small, and it quantifies asymptotically just how small they can be. This conjecture
Conjecture
A conjecture is a proposition that is unproven but is thought to be true and has not been disproven. Karl Popper pioneered the use of the term "conjecture" in scientific philosophy. Conjecture is contrasted by hypothesis , which is a testable statement based on accepted grounds...
has not been proven or disproven.
Heuristic justification
Cramér's conjecture is based on a probabilisticProbability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
model (essentially a heuristic
Heuristic
Heuristic refers to experience-based techniques for problem solving, learning, and discovery. Heuristic methods are used to speed up the process of finding a satisfactory solution, where an exhaustive search is impractical...
) of the primes, in which one assumes that the probability that a natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
x is prime is 1/log x. This is known as the Cramér model of the primes.
Cramér proved that in this model, the above conjecture holds true with probability one.
Proven results on prime gaps
Cramér also gave much weaker conditional proofConditional proof
A conditional proof is a proof that takes the form of asserting a conditional, and proving that the antecedent of the conditional necessarily leads to the consequent....
that
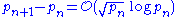
on the assumption of the Riemann hypothesis
Riemann hypothesis
In mathematics, the Riemann hypothesis, proposed by , is a conjecture about the location of the zeros of the Riemann zeta function which states that all non-trivial zeros have real part 1/2...
.
In the other direction, E. Westzynthius proved in 1931 that prime gaps grow more than logarithmically. That is,
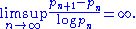
Cramér-Granville conjecture
Daniel ShanksDaniel Shanks
Daniel Shanks was an American mathematician who worked primarily in numerical analysis and number theory. He is best known as the first to compute π to 100,000 decimal places, and for his book Solved and Unsolved Problems in Number Theory.-Life and education:Dan Shanks was born on January 17,...
conjectured asymptotic equality of record gaps, a somewhat stronger statement than Cramér's conjecture.
In the random model,
 with
with 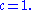
But this constant,
 , may not apply to all the primes, by Maier's theorem
, may not apply to all the primes, by Maier's theoremMaier's theorem
In number theory, Maier's theorem is a theorem about the numbers of primes in short intervals for which the Cramér's probabilistic model of primes gives the wrong answer.It states that if π is the prime counting function and λ is greater than 1 then...
. Andrew Granville
Andrew Granville
Andrew James Granville is a British mathematician, working in the field of number theory.He has been a faculty member at the Université de Montréal since 2002. Before moving to Montreal he was a mathematics professor at University of Georgia from 1991 until 2002...
in 1995 proposed the constant
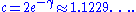
Thomas Nicely has calculated many large prime gaps. He measures the quality of fit to Cramér's conjecture by measuring the ratio R of the logarithm of a prime to the square root of the gap; he writes, “For the largest known maximal gaps, R has remained near 1.13,” showing that, at least within the range of his calculation, the Granville refinement of Cramér's conjecture seems to be a good fit to the data.
See also
- Prime number theoremPrime number theoremIn number theory, the prime number theorem describes the asymptotic distribution of the prime numbers. The prime number theorem gives a general description of how the primes are distributed amongst the positive integers....
- Legendre's conjectureLegendre's conjectureLegendre's conjecture, proposed by Adrien-Marie Legendre, states that there is a prime number between n2 and 2 for every positive integer n. The conjecture is one of Landau's problems and unproven ....
and Andrica's conjecture, much weaker but still unproven upper bounds on prime gaps

