Counting Single Transferable Votes
Encyclopedia
The single transferable vote
(STV) is a voting system
based on proportional representation
and preferential voting
. Under STV, an elector
's vote is initially allocated to his or her most-preferred candidate. After candidates have been either elected (winners) by reaching quota or eliminated (losers), surplus votes are transferred from winners to remaining candidates (hopefuls) according to the surplus ballots' ordered preferences.
The system minimizes "wasted" votes
, provides approximately proportional representation, and enables votes to be explicitly cast for individual candidates rather than for closed party lists. A variety of algorithm
s (methods) carry out these transfers.
and the Droop quota
are commonly used to determine the quota.
Except in the unlikely event that each successful candidate receives exactly the same number of votes) not enough candidates can meet the quota and fill the available seats in one count. Thus the last candidate cannot not meet the quota, and it may be fairer to eliminate that candidate.
To avoid this situation, it is common instead to use the Droop quota, which is always lower than the Hare quota.
which given as:
Droop produces a lower quota than Hare. If each ballot has a full list of preferences, Droop guarantees that every winner meets the quota rather than being elected as the last remaining candidate after lower candidates are eliminated. The fractional part of the resulting number, if any, is dropped (the result is rounded down to the next whole number.)
It is only necessary to allocate enough votes to ensure that no other candidate still in contention could win. This leaves nearly one quota's worth of votes unallocated, but counting these would not alter the outcome.
Droop is the only whole-number threshold for which (a) a majority of the voters can be guaranteed to elect a majority of the seats when there is an odd number of seats; (b) for a fixed number of seats.
Each winner's surplus votes transfer to other candidates according to their remaining preferences. Meek's counting method recomputes the quota on each iteration of the count.
The quota is calculated as
.
In the first round, Andrea receives 40 votes and Delilah 17. Andrea is
elected with 20 surplus votes. Ignoring how the votes are valued for this example, 20 votes are reallocated according to their second preferences. 12 of the reallocated votes go to Carter, 8 to Brad.
As none of the hopefuls have reached the quota, Brad, the candidate with the fewest votes, is excluded. All of his votes have Carter as the next-place choice, and are reallocated to Carter. This gives Carter 20 votes and he fills the second seat.
Thus:
The possible algorithms for doing this differ in detail, e.g., in the order of the steps. There is no general agreement on which is best, and the choice of exact method may affect the outcome.
If all seats have winners, the process is complete. Otherwise:
s, surplus votes are transferred to other candidates. The number of surplus votes is known; but none of the various allocation methods is universally preferred. Alternatives exist for deciding which votes to transfer, how to weight the transfers, who receives the votes and the order in which surpluses from two or more winners are transferred. Reallocation occurs when a candidate receives more votes than necessary to meet the quota. The excess votes are reallocated to still other candidates.
, votes are counted one precinct
at a time, imposing a spurious ordering on the votes. To prevent all transferred ballots coming from the same precinct, every
th ballot is selected, where 
is the fraction to be selected.
elections in the Republic of Ireland
. Exhausted ballots cannot be reallocated, and therefore do not contribute to any candidate.
(where every 11th vote is selected for transfer). This method is more likely than Hare to be representative, and less likely to suffer from exhausted ballots. The starting point for counting to eleven is arbitrary. Under a recount the same sample and starting point is used in the recount (i.e. the recount must only be to check for mistakes in the original count, and not a second selection of votes).
Hare and Cincinnati have the same effect for first-count winners, since all the winners' votes are in the "last batch received" from which the Hare surplus is drawn.
For each successful candidate, set aside exhausted ballots. Calculate the ratio of that candidate's surplus votes (i.e. the excess over the quota) divided by the total number of votes for that candidate, including the value of previous transfers. Transfer that candidate's votes to each voter's next preferred hopeful. Increase the recipient's vote tally by the product of the ratio and the ballot's value as the previous transfer (1 for the initial count.)
The UK's Electoral Reform Society
recommends essentially this method. Every preference continues to count until the choices on that ballot have been exhausted or the election is complete. Its main disadvantage is that given large numbers of votes, candidates and/or seats, counting is administratively burdensome.
In May to June 2011 The Proportional Representation Society of Australia
reviewed the Wright System noting:
Example: If Q is 200 and a winner has 272 first-choice votes, of which 92 have no other hopeful listed, surplus is 72, ratio is 72/(272-92) or .4. If 75 of the reassigned 180 ballots have hopeful X as their second-choice, and if X has 190 votes, then X becomes a winner, with a surplus of 20 for the next round, if needed.
The Australian variant of step 7 treats the loser's votes as though they were surplus votes. But redoing the whole method prevents what is perhaps the only significant way of gaming this system – some voters put first a candidate they are sure will be eliminated early, hoping that their later preferences will then have more influence on the outcome.
) eliminates all randomness. Instead of transferring a fraction of votes at full value, transfer all votes at a fractional value.
In the above example, the relevant fraction is
. Note that part of the 272 vote result may be from earlier transfers; e.g. perhaps Y had been elected with 250 votes, 150 with X as next preference, so that the previous transfer of 30 votes was actually 150 ballots at a value of 
. In this case, these 150 ballots would now be retransferred with a compounded fractional value of 
.
In the Republic of Ireland
Gregory is used only for the Senate, whose franchise is restricted to approximately 1,500 councillors
and members of Parliament. However, in Northern Ireland
beginning in 1973, Gregory was used for all STV elections, with up to 7 fractional transfers (in 8-seat district council elections), and up to 700,000 votes counted (in 3-seat European Parliament
elections).
An alternative means of expressing Gregory in calculating the Surplus Transfer Value applied to each vote is
Alternatively the vote could be transferred to that winner and the process continued. For example, a prior winner X could receive 20 transfers from second round winner Y. Then select 20 at random from the 220 for transfer from X. However, some of these 20 ballots may then transfer back from X to Y, creating recursion
. In the case of the Senatorial rules, since all votes are transferred at all stages, the recursion is infinite, with ever-decreasing fractions.
based on Senatorial rules, which uses an iterative approximation to short-circuit this infinite recursion. This system is currently used for some local elections in New Zealand
.
All candidates are allocated one of three statuses – Hopeful, Elected, or Excluded. Hopeful is the default. Each status has a weighting, or keep value, which is the fraction of the vote a candidate will receive for any preferences allocated to them while holding that status.
The weightings are:
Thus, if a candidate is Hopeful they retain the whole of the remaining preferences allocated to them, and subsequent preferences are worth 0.
If a candidate is Elected they retain the portion of the value of the preferences allocated to them that is the value of their weighting; the remainder is passed fractionally to subsequent preferences depending on their weighting, using the formula:
For example, consider a ballot with top preferences A, B, C, where the weightings of the three candidates are
, 
, 
respectively. From this ballot A will retain 
, B will retain 
, and C will retain 
.
This may result in a fractional excess, which is disposed of by altering the quota. Meek's method is the only method to change quota mid-process. The quota is found by
a variation on Droop. This has the effect of also altering the weighting for each candidate.
This process continues until all the Elected candidates' vote values closely match the quota (plus or minus .0001%).
Consider again a ballot with top preferences A, B, C, where the weightings are a, b, and c. Under Warren's method, A will retain a, B will retain b (or (1-a) if (1-a)
Because candidates receive different values of votes, the weightings determined by Warren are in general different than Meek.
Under Warren, every vote that contributes to a candidate contributes, as far as it is able, the same portion as every other such vote.
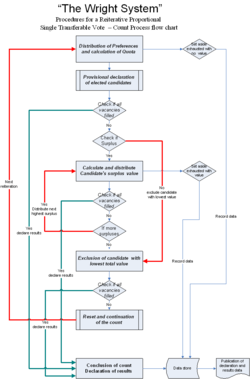In 2008, concerned about the distortion and lack of proportionality in the current Australian proportional counting systems, systems analyst
and programmer
Anthony van der Craats proposed to the Victorian and Australian Parliaments the adoption of the Wright system
(named after Jack Wright, author of the book Mirror of a Nation's Mind and past president of the Proportional Representation Society of Australia
) as an alternative counting technique.
Wright is a refinement of the Australian Senate system that replaces the method of distribution and segmentation of preferences with a reiterative linear counting system where the count is reset and restarted each time a candidate is declared a loser.
Wright fulfills the two principles identified by Meek
Wright adopts Droop Quota
(the integer value of the total number of votes divided by the number of vacant positions plus one) and the Gregory method of weighted surplus transfer. The transfer value is then multiplied by the value of each vote received by the candidates whose votes are to be redistributed, as is the case in the Western Australian upper-house elections.
Wright proposes an iterative counting process that differs from Meek in method of segmentation and distribution of losers' votes.
On every exclusion of a candidate from the count, the count is reset and all valid votes are redistributed to hopefuls.
In each iteration votes are first distributed according to each ballot's next available preference, with each vote assigned a value of one and the total number of votes tabulated for each candidate and the quota calculated on the value of the total number of valid votes using the Droop quota method.
Any candidate that reaches quota is provisionally declared elected and those ballots' surplus values are distributed according to the ballots' subsequent preference. If all seats are filled in the first count, the count is over.
If vacancies remain after all surplus votes are distributed then the candidate with the lowest tally becomes a loser. Distribution restarts following the next available preference allocated to a hopeful. This process repeats itself until all vacancies are filled in a single count without further exclusions.
Wright incorporates optional preferential voting in that any votes that do not express a valid preference for a continuing candidate are set aside and the quota is recalculated on each iteration of the count following the distribution of surplus ballots. Ballots that exhaust as a result of surplus transfer are set aside along with the value associated with the transfer in which they exhausted.
Wright's main advantage is that each vote has proportionally equal weight and is treated in the same manner as every other vote.
Under the Australian Senate system a ballot whose first preference is for a minor candidate and whose second preference is for a major candidate who won in the first count is set aside for subsequent counts. Under Wright the voter's second preference is counted and is redistributed.
The general principle that applies to each method is to exclude the candidate that has the lowest tally. Systems must handle ties for the lowest tally. Alternatives include excluding the candidate with the lowest score in the previous round and choosing by lot.
Exclusion methods commonly in use:
To determine a breakpoint, list in descending order each candidates' tally and calculate the running tally of all candidates' votes that are less than the associated candidates tally.
The four types are:
Quota breakpoints may not apply with optional preferential ballots or if more than one seat is open. Candidates above the applied breakpoint should not be included in a bulk exclusion process unless it is an adjacent quota or running breakpoint (See 2007 Tasmanian Senate count example below).
Running Breakpoint (Based on the 2007 Tasmanian Senate election results just prior to the first exclusion)
Single transferable vote
The single transferable vote is a voting system designed to achieve proportional representation through preferential voting. Under STV, an elector's vote is initially allocated to his or her most preferred candidate, and then, after candidates have been either elected or eliminated, any surplus or...
(STV) is a voting system
Voting system
A voting system or electoral system is a method by which voters make a choice between options, often in an election or on a policy referendum....
based on proportional representation
Proportional representation
Proportional representation is a concept in voting systems used to elect an assembly or council. PR means that the number of seats won by a party or group of candidates is proportionate to the number of votes received. For example, under a PR voting system if 30% of voters support a particular...
and preferential voting
Preferential voting
Preferential voting is a type of ballot structure used in several electoral systems in which voters rank candidates in order of relative preference. For example, the voter may select their first choice as '1', their second preference a '2', and so on...
. Under STV, an elector
Elector
Elector may refer to:* Prince-elector or elector, a member of the electoral college of the Holy Roman Empire, having the function of electing the Holy Roman Emperors...
's vote is initially allocated to his or her most-preferred candidate. After candidates have been either elected (winners) by reaching quota or eliminated (losers), surplus votes are transferred from winners to remaining candidates (hopefuls) according to the surplus ballots' ordered preferences.
The system minimizes "wasted" votes
Wasted vote
In the study of electoral systems, a wasted vote may be defined in two different ways:# Any vote which is not for an elected candidate.# Any vote which does not help to elect a candidate....
, provides approximately proportional representation, and enables votes to be explicitly cast for individual candidates rather than for closed party lists. A variety of algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
s (methods) carry out these transfers.
Voting
When using an STV ballot, the voter ranks the candidates on the ballot. For example:| 2 | Andrea |
| 1 | Maskill |
| 4 | Brad |
| 3 | Delilah |
Quota
The quota (sometimes called the threshold) is the number of votes a candidate must receive to be elected. The Hare quotaHare quota
The Hare quota is a formula used under some forms of the Single Transferable Vote system and the largest remainder method of party-list proportional representation...
and the Droop quota
Droop Quota
The Droop quota is the quota most commonly used in elections held under the Single Transferable Vote system. It is also sometimes used in elections held under the largest remainder method of party-list proportional representation . In an STV election the quota is the minimum number of votes a...
are commonly used to determine the quota.
Hare quota
When Thomas Hare originally conceived his version of Single Transferable Vote, he envisioned using the quota: |
| The Hare Quota |
|---|
Except in the unlikely event that each successful candidate receives exactly the same number of votes) not enough candidates can meet the quota and fill the available seats in one count. Thus the last candidate cannot not meet the quota, and it may be fairer to eliminate that candidate.
To avoid this situation, it is common instead to use the Droop quota, which is always lower than the Hare quota.
Droop quota
The most common quota formula is the Droop quotaDroop Quota
The Droop quota is the quota most commonly used in elections held under the Single Transferable Vote system. It is also sometimes used in elections held under the largest remainder method of party-list proportional representation . In an STV election the quota is the minimum number of votes a...
which given as:
-
The Droop Quota
Droop produces a lower quota than Hare. If each ballot has a full list of preferences, Droop guarantees that every winner meets the quota rather than being elected as the last remaining candidate after lower candidates are eliminated. The fractional part of the resulting number, if any, is dropped (the result is rounded down to the next whole number.)
It is only necessary to allocate enough votes to ensure that no other candidate still in contention could win. This leaves nearly one quota's worth of votes unallocated, but counting these would not alter the outcome.
Droop is the only whole-number threshold for which (a) a majority of the voters can be guaranteed to elect a majority of the seats when there is an odd number of seats; (b) for a fixed number of seats.
Each winner's surplus votes transfer to other candidates according to their remaining preferences. Meek's counting method recomputes the quota on each iteration of the count.
Example
Two seats need to be filled among four candidates: Andrea, Brad, Carter, and Delilah. 57 voters cast ballots with the following preference orderings:| 16 Votes | 24 Votes | 17 Votes | |
| 1st | Andrea | Andrea | Delilah |
| 2nd | Brad | Carter | Andrea |
| 3rd | Carter | Brad | Brad |
| 4th | Delilah | Delilah | Carter |
The quota is calculated as
.In the first round, Andrea receives 40 votes and Delilah 17. Andrea is
elected with 20 surplus votes. Ignoring how the votes are valued for this example, 20 votes are reallocated according to their second preferences. 12 of the reallocated votes go to Carter, 8 to Brad.
As none of the hopefuls have reached the quota, Brad, the candidate with the fewest votes, is excluded. All of his votes have Carter as the next-place choice, and are reallocated to Carter. This gives Carter 20 votes and he fills the second seat.
Thus:
| Round 1 | Round 2 | Round 3 | ||
| Andrea | 40 | 20 | 20 | Elected in round 1 |
| Brad | 0 | 8 | 0 | Excluded in round 2 |
| Carter | 0 | 12 | 20 | Elected in round 3 |
| Delilah | 17 | 17 | 17 | Defeated in round 3 |
Counting rules
Under the single transferable vote system, votes are successively transferred to hopefuls from two sources:- Surplus votes (i.e. those in excess of the quota) of successful candidates
- All votes of eliminated candidates.
The possible algorithms for doing this differ in detail, e.g., in the order of the steps. There is no general agreement on which is best, and the choice of exact method may affect the outcome.
- Compute the quota.
- Assign votes to candidates by first preferences.
- Declare as winners all candidates who received at least the quota.
- Transfer the excess votes from winners to hopefuls.
- Repeat 2-4 until no new candidates are elected. (Under some systems, votes could initially be transferred in this step to prior winners or losers. This might affect the outcome.)
If all seats have winners, the process is complete. Otherwise:
- Eliminate one or more candidates. Typically either the lowest candidate or all candidates whose combined votes are less than the vote of the lowest remaining candidate.
- Transfer the votes of the losers to continuing candidates are declared to be losers.
- Repeat 2-7 until all seats are full.
Surplus allocation
To minimize wasted voteWasted vote
In the study of electoral systems, a wasted vote may be defined in two different ways:# Any vote which is not for an elected candidate.# Any vote which does not help to elect a candidate....
s, surplus votes are transferred to other candidates. The number of surplus votes is known; but none of the various allocation methods is universally preferred. Alternatives exist for deciding which votes to transfer, how to weight the transfers, who receives the votes and the order in which surpluses from two or more winners are transferred. Reallocation occurs when a candidate receives more votes than necessary to meet the quota. The excess votes are reallocated to still other candidates.
Random subset
Some surplus allocation methods select a random vote sample. Sometimes, ballots of one elected candidate are manually mixed. In Cambridge, MassachusettsCambridge, Massachusetts
Cambridge is a city in Middlesex County, Massachusetts, United States, in the Greater Boston area. It was named in honor of the University of Cambridge in England, an important center of the Puritan theology embraced by the town's founders. Cambridge is home to two of the world's most prominent...
, votes are counted one precinct
Precinct
A precinct is a space enclosed by the walls or other boundaries of a particular place or building, or by an arbitrary and imaginary line drawn around it. The term has several different uses...
at a time, imposing a spurious ordering on the votes. To prevent all transferred ballots coming from the same precinct, every
th ballot is selected, where is the fraction to be selected.Hare
Reallocation ballots are drawn at random from those transferred. In a manual count of paper ballots, this is the easiest method to implement; it is close to Thomas Hare's original 1857 proposal. It is used in all universal suffrageUniversal suffrage
Universal suffrage consists of the extension of the right to vote to adult citizens as a whole, though it may also mean extending said right to minors and non-citizens...
elections in the Republic of Ireland
Republic of Ireland
Ireland , described as the Republic of Ireland , is a sovereign state in Europe occupying approximately five-sixths of the island of the same name. Its capital is Dublin. Ireland, which had a population of 4.58 million in 2011, is a constitutional republic governed as a parliamentary democracy,...
. Exhausted ballots cannot be reallocated, and therefore do not contribute to any candidate.
Cincinnati
Reallocation ballots are drawn at random from all of the candidate's votes. This method is used in Cambridge, MassachusettsCambridge, Massachusetts
Cambridge is a city in Middlesex County, Massachusetts, United States, in the Greater Boston area. It was named in honor of the University of Cambridge in England, an important center of the Puritan theology embraced by the town's founders. Cambridge is home to two of the world's most prominent...
(where every 11th vote is selected for transfer). This method is more likely than Hare to be representative, and less likely to suffer from exhausted ballots. The starting point for counting to eleven is arbitrary. Under a recount the same sample and starting point is used in the recount (i.e. the recount must only be to check for mistakes in the original count, and not a second selection of votes).
Hare and Cincinnati have the same effect for first-count winners, since all the winners' votes are in the "last batch received" from which the Hare surplus is drawn.
Wright's
This is a simplified explanation of the Wright System below.For each successful candidate, set aside exhausted ballots. Calculate the ratio of that candidate's surplus votes (i.e. the excess over the quota) divided by the total number of votes for that candidate, including the value of previous transfers. Transfer that candidate's votes to each voter's next preferred hopeful. Increase the recipient's vote tally by the product of the ratio and the ballot's value as the previous transfer (1 for the initial count.)
The UK's Electoral Reform Society
Electoral Reform Society
The Electoral Reform Society is a political pressure group based in the United Kingdom which promotes electoral reform. It is believed to be the oldest organisation concerned with electoral systems in the world.-Aims:...
recommends essentially this method. Every preference continues to count until the choices on that ballot have been exhausted or the election is complete. Its main disadvantage is that given large numbers of votes, candidates and/or seats, counting is administratively burdensome.
In May to June 2011 The Proportional Representation Society of Australia
Proportional Representation Society of Australia
The Proportional Representation Society of Australia is one of the main electoral reform organisations in Australia. It has branches in South Australia, Victoria-Tasmania, New South Wales, Western Australia and the Australian Capital Territory...
reviewed the Wright System noting:
Hare-Clark
This is a variation on the original Hare method which used random choices. It is used in elections in Australia. It allows votes to the same ballots to repeatedly transferred. In the following explanation, Q is the quota required for election.- Separate all ballots according to their first preferences.
- Count the votes.
- Declare as winners those hopefuls whose total is at least Q.
- For each winner, compute surplus as total minus Q.
- For each winner, in order of descending surplus:
- Assign that candidate's ballots to hopefuls according to each ballot's preference, setting aside exhausted ballots.
- Calculate the ratio of surplus to the number of reassigned ballots or 1 if the number of such ballots is less than surplus.
- For each hopeful, multiply ratio * the number of that hopeful's reassigned votes and add the result (rounded down) to the hopeful's tally.
- Repeat 3-5 until winners fill all seats, or all ballots are exhausted.
- If more winners are needed, declare a loser the hopeful with the fewest votes, recompute Q and repeat from 1, ignoring all preferences for the loser.
Example: If Q is 200 and a winner has 272 first-choice votes, of which 92 have no other hopeful listed, surplus is 72, ratio is 72/(272-92) or .4. If 75 of the reassigned 180 ballots have hopeful X as their second-choice, and if X has 190 votes, then X becomes a winner, with a surplus of 20 for the next round, if needed.
The Australian variant of step 7 treats the loser's votes as though they were surplus votes. But redoing the whole method prevents what is perhaps the only significant way of gaming this system – some voters put first a candidate they are sure will be eliminated early, hoping that their later preferences will then have more influence on the outcome.
Gregory
Another method, known as Senatorial rules (after its use for most seats in Irish Senate elections), or Gregory method (after its inventor in 1880, J.B. Gregory of MelbourneMelbourne
Melbourne is the capital and most populous city in the state of Victoria, and the second most populous city in Australia. The Melbourne City Centre is the hub of the greater metropolitan area and the Census statistical division—of which "Melbourne" is the common name. As of June 2009, the greater...
) eliminates all randomness. Instead of transferring a fraction of votes at full value, transfer all votes at a fractional value.
In the above example, the relevant fraction is
. Note that part of the 272 vote result may be from earlier transfers; e.g. perhaps Y had been elected with 250 votes, 150 with X as next preference, so that the previous transfer of 30 votes was actually 150 ballots at a value of . In this case, these 150 ballots would now be retransferred with a compounded fractional value of .In the Republic of Ireland
Republic of Ireland
Ireland , described as the Republic of Ireland , is a sovereign state in Europe occupying approximately five-sixths of the island of the same name. Its capital is Dublin. Ireland, which had a population of 4.58 million in 2011, is a constitutional republic governed as a parliamentary democracy,...
Gregory is used only for the Senate, whose franchise is restricted to approximately 1,500 councillors
County council
A county council is the elected administrative body governing an area known as a county. This term has slightly different meanings in different countries.-United Kingdom:...
and members of Parliament. However, in Northern Ireland
Northern Ireland
Northern Ireland is one of the four countries of the United Kingdom. Situated in the north-east of the island of Ireland, it shares a border with the Republic of Ireland to the south and west...
beginning in 1973, Gregory was used for all STV elections, with up to 7 fractional transfers (in 8-seat district council elections), and up to 700,000 votes counted (in 3-seat European Parliament
European Parliament
The European Parliament is the directly elected parliamentary institution of the European Union . Together with the Council of the European Union and the Commission, it exercises the legislative function of the EU and it has been described as one of the most powerful legislatures in the world...
elections).
An alternative means of expressing Gregory in calculating the Surplus Transfer Value applied to each vote is
Secondary preferences for prior winners
Suppose a ballot is to be transferred and its next preference is for a winner in a prior round. Hare and Cincinnati ignore such preferences and transfer the ballot to the next preference.Alternatively the vote could be transferred to that winner and the process continued. For example, a prior winner X could receive 20 transfers from second round winner Y. Then select 20 at random from the 220 for transfer from X. However, some of these 20 ballots may then transfer back from X to Y, creating recursion
Recursion
Recursion is the process of repeating items in a self-similar way. For instance, when the surfaces of two mirrors are exactly parallel with each other the nested images that occur are a form of infinite recursion. The term has a variety of meanings specific to a variety of disciplines ranging from...
. In the case of the Senatorial rules, since all votes are transferred at all stages, the recursion is infinite, with ever-decreasing fractions.
Meek
In 1969, B.L. Meek devised an algorithmAlgorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
based on Senatorial rules, which uses an iterative approximation to short-circuit this infinite recursion. This system is currently used for some local elections in New Zealand
New Zealand
New Zealand is an island country in the south-western Pacific Ocean comprising two main landmasses and numerous smaller islands. The country is situated some east of Australia across the Tasman Sea, and roughly south of the Pacific island nations of New Caledonia, Fiji, and Tonga...
.
All candidates are allocated one of three statuses – Hopeful, Elected, or Excluded. Hopeful is the default. Each status has a weighting, or keep value, which is the fraction of the vote a candidate will receive for any preferences allocated to them while holding that status.
The weightings are:
| Hopeful |  |
| Excluded |  |
| Elected |  which is repeated until  for all elected candidates |
Thus, if a candidate is Hopeful they retain the whole of the remaining preferences allocated to them, and subsequent preferences are worth 0.
If a candidate is Elected they retain the portion of the value of the preferences allocated to them that is the value of their weighting; the remainder is passed fractionally to subsequent preferences depending on their weighting, using the formula:
For example, consider a ballot with top preferences A, B, C, where the weightings of the three candidates are
, , respectively. From this ballot A will retain , B will retain , and C will retain .This may result in a fractional excess, which is disposed of by altering the quota. Meek's method is the only method to change quota mid-process. The quota is found by
a variation on Droop. This has the effect of also altering the weighting for each candidate.
This process continues until all the Elected candidates' vote values closely match the quota (plus or minus .0001%).
Warren
In 1994, C.H.E. Warren proposed another method of passing surplus to previously-elected candidates. Warren is identical to Meek except in the amounts of votes retained by winners. Under Warren, rather than retaining that proportion of each vote's value given by multiplying the weighting by the vote's value, the candidate retains that amount of a whole vote given by the weighting, or else whatever remains of the vote's value if that is less than the weighting.Consider again a ballot with top preferences A, B, C, where the weightings are a, b, and c. Under Warren's method, A will retain a, B will retain b (or (1-a) if (1-a)
Because candidates receive different values of votes, the weightings determined by Warren are in general different than Meek.
Under Warren, every vote that contributes to a candidate contributes, as far as it is able, the same portion as every other such vote.
Wright
Systems analyst
A systems analyst researches problems, plans solutions, recommends software and systems, and coordinates development to meet business or other requirements. They will be familiar with multiple variety of programming languages, operating systems, and computer hardware platforms...
and programmer
Programmer
A programmer, computer programmer or coder is someone who writes computer software. The term computer programmer can refer to a specialist in one area of computer programming or to a generalist who writes code for many kinds of software. One who practices or professes a formal approach to...
Anthony van der Craats proposed to the Victorian and Australian Parliaments the adoption of the Wright system
Wright system
The Wright system is a refinement of rules associated with proportional representation by means of the single transferable vote electoral system...
(named after Jack Wright, author of the book Mirror of a Nation's Mind and past president of the Proportional Representation Society of Australia
Proportional Representation Society of Australia
The Proportional Representation Society of Australia is one of the main electoral reform organisations in Australia. It has branches in South Australia, Victoria-Tasmania, New South Wales, Western Australia and the Australian Capital Territory...
) as an alternative counting technique.
Wright is a refinement of the Australian Senate system that replaces the method of distribution and segmentation of preferences with a reiterative linear counting system where the count is reset and restarted each time a candidate is declared a loser.
Wright fulfills the two principles identified by Meek
- Once a candidate is eliminated, all ballots are treated as if that candidate had never stood.
- Winners retain a fixed proportion of every vote received, and transfer the remainder to the next preference for a hopeful.
Wright adopts Droop Quota
Droop Quota
The Droop quota is the quota most commonly used in elections held under the Single Transferable Vote system. It is also sometimes used in elections held under the largest remainder method of party-list proportional representation . In an STV election the quota is the minimum number of votes a...
(the integer value of the total number of votes divided by the number of vacant positions plus one) and the Gregory method of weighted surplus transfer. The transfer value is then multiplied by the value of each vote received by the candidates whose votes are to be redistributed, as is the case in the Western Australian upper-house elections.
Wright proposes an iterative counting process that differs from Meek in method of segmentation and distribution of losers' votes.
On every exclusion of a candidate from the count, the count is reset and all valid votes are redistributed to hopefuls.
In each iteration votes are first distributed according to each ballot's next available preference, with each vote assigned a value of one and the total number of votes tabulated for each candidate and the quota calculated on the value of the total number of valid votes using the Droop quota method.
Any candidate that reaches quota is provisionally declared elected and those ballots' surplus values are distributed according to the ballots' subsequent preference. If all seats are filled in the first count, the count is over.
If vacancies remain after all surplus votes are distributed then the candidate with the lowest tally becomes a loser. Distribution restarts following the next available preference allocated to a hopeful. This process repeats itself until all vacancies are filled in a single count without further exclusions.
Wright incorporates optional preferential voting in that any votes that do not express a valid preference for a continuing candidate are set aside and the quota is recalculated on each iteration of the count following the distribution of surplus ballots. Ballots that exhaust as a result of surplus transfer are set aside along with the value associated with the transfer in which they exhausted.
Wright's main advantage is that each vote has proportionally equal weight and is treated in the same manner as every other vote.
Under the Australian Senate system a ballot whose first preference is for a minor candidate and whose second preference is for a major candidate who won in the first count is set aside for subsequent counts. Under Wright the voter's second preference is counted and is redistributed.
Distribution of excluded candidate preferences
The method used in determining the order of exclusion and distribution of a candidates' votes can affect the outcome. Multiple methods are in common use for determining the order polyexclusion and distribution of ballots from a loser. Most systems (with the exception of an iterative count) were designed for manual counting processes and can produce different outcomes.The general principle that applies to each method is to exclude the candidate that has the lowest tally. Systems must handle ties for the lowest tally. Alternatives include excluding the candidate with the lowest score in the previous round and choosing by lot.
Exclusion methods commonly in use:
- Single transaction—Transfer all votes for a loser in a single transaction without segmentation.
- Segmented distribution—Split distributed ballots into small, segmented transactions. Consider each segment a complete transaction, including checking for candidates who have reached quota. Generally, a smaller number and value of votes per segment reduces the likelihood of affecting the outcome.
- Value based segmentation—Each segment includes all ballots that have the same value.
- Aggregated primary vote and value segmentation—Separate the Primary vote (full-value votes) to reduce distortion and limit the subsequent value of a transfer from a candidate elected as result of a segmented transfer.
- FIFO (First In First Out - Last bundle)—Distribute each parcel in the order in which it was received. This method produces the smallest size and impact of each segment at the cost of requiring more steps to complete a count.
- Iterative count—After excluding a loser, reallocate the loser's ballots and restart the count. An iterative count treats each ballot as though that loser had not stood. Ballots can be allocated to prior winners using a segmented distribution process. Surplus votes are distributed only within each iteration. Iterative counts are usually automated to reduce costs. The number of iterations can be limited by applying a method of Bulk Exclusion.
Bulk exclusions
Bulk exclusion rules can reduce the number of steps required within a count. Bulk exclusion requires the calculation of breakpoints. Any candidates with a tally less than a breakpoint can be included in a bulk exclusion process provided the value of the associated running sum is not greater than the difference between the total value of the highest hopeful's tally and the quota.To determine a breakpoint, list in descending order each candidates' tally and calculate the running tally of all candidates' votes that are less than the associated candidates tally.
The four types are:
- Quota Breakpoint—The highest running total value that is less than half of the Quota
- Running Breakpoint—The highest candidate's tally that is less than the associated running total
- Group Breakpoint—The highest candidate's tally in a Group that is less than the associated running total of Group candidates whose tally is less than the associated Candidate's tally. (This only applies where there are defined groups of candidates such as in Australian public elections which use an Above-the-line group voting method.)
- Applied Breakpoint—The highest running total that is less than the difference between the highest candidate's tally and the quota (i.e. the tally of lower-scoring candidates votes does not effect the outcome). All candidates above an applied breakpoint continue in the next iteration.
Quota breakpoints may not apply with optional preferential ballots or if more than one seat is open. Candidates above the applied breakpoint should not be included in a bulk exclusion process unless it is an adjacent quota or running breakpoint (See 2007 Tasmanian Senate count example below).
Example
Quota Breakpoint (Based on the 2007 Queensland Senate election results just prior to the first exclusion)| Candidate | Ballot position | GroupAb | Group name | Score | Running sum | Breakpoint / Status |
|---|---|---|---|---|---|---|
| MACDONALD, Ian Douglas | J-1 | LNP | Liberal | 345559 | Quota | |
| HOGG, John Joseph | O-1 | ALP | Australian Labor Party | 345559 | Quota | |
| BOYCE, Sue | J-2 | LNP | Liberal | 345559 | Quota | |
| MOORE, Claire | O-2 | ALP | Australian Labor Party | 345559 | Quota | |
| BOSWELL, Ron | J-3 | LNP | Liberal | 284488 | 539459 | Contest |
| WATERS, Larissa | O-3 | ALP | The Greens | 254971 | 431482 | Contest |
| FURNER, Mark | M-1 | GRN | Australian Labor Party | 176511 | 278103 | Contest |
| HANSON, Pauline | R-1 | HAN | Pauline | 101592 | 154430 | Contest |
| BUCHANAN, Jeff | H-1 | FFP | Family First | 52838 | 98233 | Contest |
| BARTLETT, Andrew | I-1 | DEM | Democrats | 45395 | 65672 | Contest |
| SMITH, Bob | G-1 | AFLP | The Fishing Party | 20277 | 39358 | Quota Breakpoint |
| COLLINS, Kevin | P-1 | FP | Australian Fishing and Lifestyle Party | 19081 | 36364 | Contest |
| BOUSFIELD, Anne | A-1 | WWW | What Women Want (Australia) | 17283 | 30140 | Contest |
| FEENEY, Paul Joseph | L-1 | ASP | The Australian Shooters Party | 12857 | 21559 | Contest |
| JOHNSON, Phil | C-1 | CCC | Climate Change Coalition | 8702 | 15957 | Contest |
| JACKSON, Noel | V-1 | DLP | D.L.P. - Democratic Labor Party | 7255 | 49932 | Applied Breakpoint |
| Others | 42677 | 42677 |
Running Breakpoint (Based on the 2007 Tasmanian Senate election results just prior to the first exclusion)
| Candidate | Ballot position | GroupAb | Group name | Score | Running sum | Breakpoint / Status |
|---|---|---|---|---|---|---|
| SHERRY, Nick | D-1 | ALP | Australian Labor Party | 46693 | Quota | |
| COLBECK, Richard M | F-1 | LP | Liberal | 46693 | Quota | |
| BROWN, Bob | B-1 | GRN | The Greens | 46693 | Quota | |
| BROWN, Carol | D-2 | ALP | Australian Labor Party | 46693 | Quota | |
| BUSHBY, David | F-2 | LP | Liberal | 46693 | Quota | |
| BILYK, Catryna | D-3 | ALP | Australian Labor Party | 37189 | Contest | |
| MORRIS, Don | F-3 | LP | Liberal | 28586 | Contest | |
| WILKIE, Andrew | B-2 | GRN | The Greens | 12193 | 27607 | Running Breakpoint |
| PETRUSMA, Jacquie | K-1 | FFP | Family First | 6471 | 15414 | Quota Breakpoint |
| CASHION, Debra | A-1 | WWW | What Women Want (Australia) | 2487 | 8943 | Applied Breakpoint |
| CREA, Pat | E-1 | DLP | D.L.P. - Democratic Labor Party | 2027 | 6457 | |
| OTTAVI, Dino | G-1 | UN3 | 1347 | 4430 | ||
| MARTIN, Steve | C-1 | UN1 | 848 | 3083 | ||
| HOUGHTON, Sophie Louise | B-3 | GRN | The Greens | 353 | 2236 | |
| LARNER, Caroline | J-1 | CEC | Citizens Electoral Council | 311 | 1883 | |
| IRELAND, Bede | I-1 | LDP | LDP | 298 | 1573 | |
| DOYLE, Robyn | H-1 | UN2 | 245 | 1275 | ||
| BENNETT, Andrew | K-2 | FFP | Family First | 174 | 1030 | |
| ROBERTS, Betty | K-3 | FFP | Family First | 158 | 856 | |
| JORDAN, Scott | B-4 | GRN | The Greens | 139 | 698 | |
| GLEESON, Belinda | A-2 | WWW | What Women Want (Australia) | 135 | 558 | |
| SHACKCLOTH, Joan | E-2 | DLP | D.L.P. - Democratic Labor Party | 116 | 423 | |
| SMALLBANE, Chris | G-3 | UN3 | 102 | 307 | ||
| COOK, Mick | G-2 | UN3 | 74 | 205 | ||
| HAMMOND, David | H-2 | UN2 | 53 | 132 | ||
| NELSON, Karley | C-2 | UN1 | 35 | 79 | ||
| PHIBBS, Michael | J-2 | CEC | Citizens Electoral Council | 23 | 44 | |
| HAMILTON, Luke | I-2 | LDP | LDP | 21 | 21 |
See also
- Hagenbach-Bischoff quotaHagenbach-Bischoff quotaThe Hagenbach-Bischoff quota is a formula used in some voting systems based on proportional representation . It is used in some elections held under the largest remainder method of party-list proportional representation as well as in a variant of the D'Hondt method known as the Hagenbach-Bischoff...
- Imperiali quotaImperiali quotaThe Imperiali quota is a formula used to calculate the minimum number, or quota, of votes required to capture a seat in some forms of single transferable vote or largest remainder method party-list proportional representation voting systems....
- IRV implementations in United States#Independence Party of Minnesota (2004 Presidential poll)
- Voting mattersVoting mattersVoting matters is a peer-reviewed academic journal whose purpose is "To advance the understanding of preferential voting systems". Originally published by the Electoral Reform Society , Voting matters is now a publication of the McDougall Trust...
— To advance the understanding of preferential voting systems, McDougall Trust journal comparing and critiquing actual and theoretical varieties of STV and related voting systems.
External links
- Fair vote - US campaign for electoral reform.
- Quota Notes - Proportional Representation Society of Australia.
- Australian Electoral Commission Web site.
- Algorithm 123 — Single Transferable Vote by Meek's Method
- OpenSTV -- software for computing the single transferable vote
- Irish Proportional Representation System
- Banbridge Council election results giving detailed breakdowns of fractional transfers, illustrating Senatorial Rules.
- New Zealand's Local Electoral Act 2001 - How to count votes under Meek's method
- Animated presentation of how Meek's method is used to count votes in New Zealand STV
- Movable vote workshop tallies STV and related rules.