
Cosine similarity
Encyclopedia
Cosine similarity is a measure of similarity between two vectors by measuring the cosine of the angle between them. The cosine of 0 is 1, and less than 1 for any other angle. The cosine of the angle between two vectors thus determines whether two vectors are pointing in roughly the same direction.
This is often used to compare documents in text mining
. In addition, it is used to measure cohesion within clusters in the field of Data Mining
.
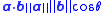
Given two vectors of attributes, A and B, the cosine similarity, θ, is represented using a dot product
and magnitude as
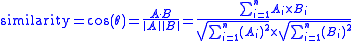
The resulting similarity ranges from −1 meaning exactly opposite, to 1 meaning exactly the same, with 0 usually indicating independence, and in-between values indicating intermediate similarity or dissimilarity.
For text matching, the attribute vectors A and B are usually the term frequency vectors of the documents. The cosine similarity can be seen as a method of normalizing document length during comparison.
In the case of information retrieval
, the cosine similarity of two documents will range from 0 to 1, since the term frequencies (tf-idf weights) cannot be negative. The angle between two term frequency vectors cannot be greater than 90°.

in a domain where vector coefficients may be positive or negative, or
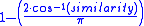
in a domain where the vector coefficients are always positive.
Although the term "cosine similarity" has been used for this angular distance, the term is oddly used as the cosine of the angle is used only as a convenient mechanism for calculating the angle itself and is no part of the meaning. The advantage of the angular similarity coefficient is that, when used as a difference coefficeint (by subtracting it from 1) the resulting function is a proper distance metric, which is not the case for the first meaning. However for most uses this is not an important property. For any use where only the relative ordering of similarity or distance within a set of vectors is important, then which function is used is immaterial as the a resulting order will be unaffected by the choice.
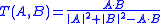
In fact, this algebraic form was first defined by Tanimoto as a mechanism for calculating the Jaccard coefficient in the case where the sets being compared are represented as bit vectors. While the formula extends to vectors in general, it has quite different properties from Cosine Similarity and bears little relation other than its superficial appearance.
This is often used to compare documents in text mining
Text mining
Text mining, sometimes alternately referred to as text data mining, roughly equivalent to text analytics, refers to the process of deriving high-quality information from text. High-quality information is typically derived through the devising of patterns and trends through means such as...
. In addition, it is used to measure cohesion within clusters in the field of Data Mining
Data mining
Data mining , a relatively young and interdisciplinary field of computer science is the process of discovering new patterns from large data sets involving methods at the intersection of artificial intelligence, machine learning, statistics and database systems...
.
Math
The cosine of two vectors can be easily derived by using the Euclidean Dot Product formula: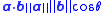
Given two vectors of attributes, A and B, the cosine similarity, θ, is represented using a dot product
Dot product
In mathematics, the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers and returns a single number obtained by multiplying corresponding entries and then summing those products...
and magnitude as
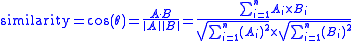
The resulting similarity ranges from −1 meaning exactly opposite, to 1 meaning exactly the same, with 0 usually indicating independence, and in-between values indicating intermediate similarity or dissimilarity.
For text matching, the attribute vectors A and B are usually the term frequency vectors of the documents. The cosine similarity can be seen as a method of normalizing document length during comparison.
In the case of information retrieval
Information retrieval
Information retrieval is the area of study concerned with searching for documents, for information within documents, and for metadata about documents, as well as that of searching structured storage, relational databases, and the World Wide Web...
, the cosine similarity of two documents will range from 0 to 1, since the term frequencies (tf-idf weights) cannot be negative. The angle between two term frequency vectors cannot be greater than 90°.
Angular similarity
The term "cosine similarity" has also been used on occasion to express a different coefficient, although the most common use is as defined above. Using the same calculation of similarity, the normalised angle between the vectors can be used as a bounded similarity function within [0,1], calculated from the above definition of similarity by:
in a domain where vector coefficients may be positive or negative, or
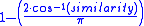
in a domain where the vector coefficients are always positive.
Although the term "cosine similarity" has been used for this angular distance, the term is oddly used as the cosine of the angle is used only as a convenient mechanism for calculating the angle itself and is no part of the meaning. The advantage of the angular similarity coefficient is that, when used as a difference coefficeint (by subtracting it from 1) the resulting function is a proper distance metric, which is not the case for the first meaning. However for most uses this is not an important property. For any use where only the relative ordering of similarity or distance within a set of vectors is important, then which function is used is immaterial as the a resulting order will be unaffected by the choice.
Confusion with "Tanimoto" coefficient
On occasion, Cosine Similarity has been confused as a specialised form of a similarity coefficeint with a similar algebraic form: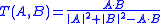
In fact, this algebraic form was first defined by Tanimoto as a mechanism for calculating the Jaccard coefficient in the case where the sets being compared are represented as bit vectors. While the formula extends to vectors in general, it has quite different properties from Cosine Similarity and bears little relation other than its superficial appearance.
See also
- Tanimoto Distance
- Sørensen's quotient of similaritySørensen similarity indexThe Sørensen index, also known as Sørensen’s similarity coefficient, is a statistic used for comparing the similarity of two samples. It was developed by the botanist Thorvald Sørensen and published in 1948....
- Hamming distanceHamming distanceIn information theory, the Hamming distance between two strings of equal length is the number of positions at which the corresponding symbols are different...
- CorrelationCorrelationIn statistics, dependence refers to any statistical relationship between two random variables or two sets of data. Correlation refers to any of a broad class of statistical relationships involving dependence....
- Dice's coefficient
- Jaccard indexJaccard indexThe Jaccard index, also known as the Jaccard similarity coefficient , is a statistic used for comparing the similarity and diversity of sample sets....
- SimRankSimRankSimRank is a general similarity measure, based on a simple and intuitive graph-theoretic model.SimRank is applicable in any domain with object-to-object relationships, that measures similarity of the structural context in which objects occur, based on their relationships with other...
- Information retrievalInformation retrievalInformation retrieval is the area of study concerned with searching for documents, for information within documents, and for metadata about documents, as well as that of searching structured storage, relational databases, and the World Wide Web...
External links
- Weighted cosine measure
- http://www.miislita.com/information-retrieval-tutorial/cosine-similarity-tutorial.html#Cosim

