
Cornacchia's algorithm
Encyclopedia
In computational number theory
, Cornacchia's algorithm is an algorithm
for solving the Diophantine equation
 , where
, where 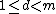 and d and m are coprime
and d and m are coprime
. The algorithm was described in 1908 by Giuseppe Cornacchia.
 ; if no such
; if no such 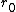 exist, there can be no solution to the original equation. Then use the Euclidean algorithm
exist, there can be no solution to the original equation. Then use the Euclidean algorithm
to find ,
,  and so on; stop when
and so on; stop when 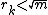 . If
. If 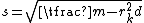 is an integer, then the solution is
is an integer, then the solution is  ; otherwise there is no solution.
; otherwise there is no solution.
 . A square root of −6 (mod 103) is 32, and 103 ≡ 7 (mod 32); since
. A square root of −6 (mod 103) is 32, and 103 ≡ 7 (mod 32); since 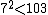 and
and 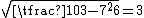 , there is a solution x = 7, y = 3.
, there is a solution x = 7, y = 3.
Computational number theory
In mathematics, computational number theory, also known as algorithmic number theory, is the study of algorithms for performing number theoretic computations...
, Cornacchia's algorithm is an algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
for solving the Diophantine equation
Diophantine equation
In mathematics, a Diophantine equation is an indeterminate polynomial equation that allows the variables to be integers only. Diophantine problems have fewer equations than unknown variables and involve finding integers that work correctly for all equations...
 , where
, where 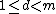 and d and m are coprime
and d and m are coprimeCoprime
In number theory, a branch of mathematics, two integers a and b are said to be coprime or relatively prime if the only positive integer that evenly divides both of them is 1. This is the same thing as their greatest common divisor being 1...
. The algorithm was described in 1908 by Giuseppe Cornacchia.
The algorithm
First, find any solution to ; if no such
; if no such 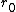 exist, there can be no solution to the original equation. Then use the Euclidean algorithm
exist, there can be no solution to the original equation. Then use the Euclidean algorithmEuclidean algorithm
In mathematics, the Euclidean algorithm is an efficient method for computing the greatest common divisor of two integers, also known as the greatest common factor or highest common factor...
to find
 ,
,  and so on; stop when
and so on; stop when 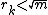 . If
. If 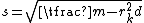 is an integer, then the solution is
is an integer, then the solution is  ; otherwise there is no solution.
; otherwise there is no solution.Example
Solve the equation . A square root of −6 (mod 103) is 32, and 103 ≡ 7 (mod 32); since
. A square root of −6 (mod 103) is 32, and 103 ≡ 7 (mod 32); since 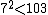 and
and 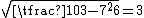 , there is a solution x = 7, y = 3.
, there is a solution x = 7, y = 3.
