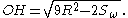Conway triangle notation
Encyclopedia
In geometry
, the Conway triangle notation, named after John Horton Conway
, allows trigonometric functions of a triangle
to be managed algebraically. Given a reference triangle whose sides are a, b and c and whose corresponding internal angle
s are A, B, and C then the Conway triangle notation is simply represented as follows:
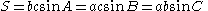
where S = 2 × area of reference triangle and
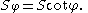
in particular
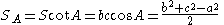
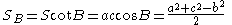

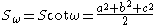 where
where 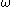 is the Brocard angle.
is the Brocard angle.

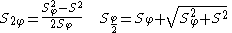 for values of
for values of  where
where 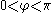

Hence:
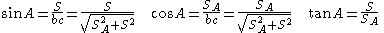
Some important identities:
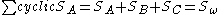
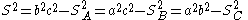
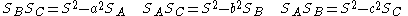
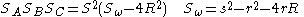
where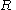 is the circumradius and
is the circumradius and 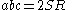 and where
and where 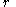 is the incenter,
is the incenter, 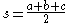 and
and 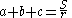
Some useful trigonometric conversions:

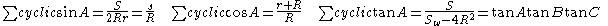
Some useful formulas:
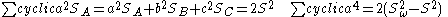
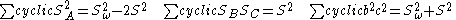
Some examples using Conway triangle notation:
Let D be the distance between two points P and Q whose trilinear coordinates
are pa : pb : pc and qa : qb : qc. Let Kp = apa + bpb + cpc and let Kq = aqa + bqb + cqc. Then D is given by the formula:
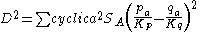
Using this formula it is possible to determine OH, the distance between the circumcenter and the orthocenter as follows:
For the circumcenter and for the orthocenter
and for the orthocenter 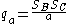

Hence:
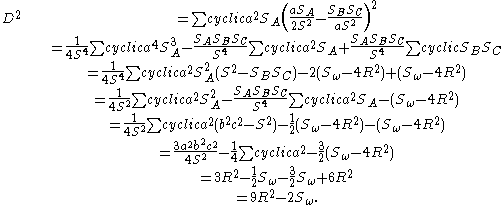
This gives:
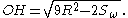
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, the Conway triangle notation, named after John Horton Conway
John Horton Conway
John Horton Conway is a prolific mathematician active in the theory of finite groups, knot theory, number theory, combinatorial game theory and coding theory...
, allows trigonometric functions of a triangle
Triangle
A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted ....
to be managed algebraically. Given a reference triangle whose sides are a, b and c and whose corresponding internal angle
Angle
In geometry, an angle is the figure formed by two rays sharing a common endpoint, called the vertex of the angle.Angles are usually presumed to be in a Euclidean plane with the circle taken for standard with regard to direction. In fact, an angle is frequently viewed as a measure of an circular arc...
s are A, B, and C then the Conway triangle notation is simply represented as follows:
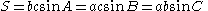
where S = 2 × area of reference triangle and
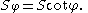
in particular
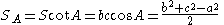
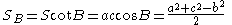

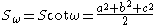 where
where 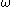 is the Brocard angle.
is the Brocard angle.
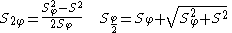 for values of
for values of  where
where 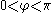

Hence:
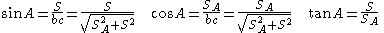
Some important identities:
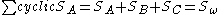
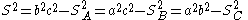
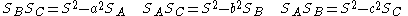
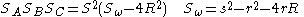
where
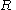 is the circumradius and
is the circumradius and 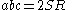 and where
and where 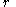 is the incenter,
is the incenter, 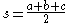 and
and 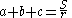
Some useful trigonometric conversions:

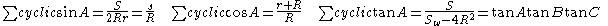
Some useful formulas:
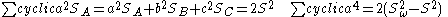
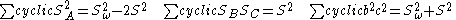
Some examples using Conway triangle notation:
Let D be the distance between two points P and Q whose trilinear coordinates
Trilinear coordinates
In geometry, the trilinear coordinates of a point relative to a given triangle describe the relative distances from the three sides of the triangle. Trilinear coordinates are an example of homogeneous coordinates...
are pa : pb : pc and qa : qb : qc. Let Kp = apa + bpb + cpc and let Kq = aqa + bqb + cqc. Then D is given by the formula:
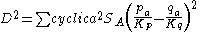
Using this formula it is possible to determine OH, the distance between the circumcenter and the orthocenter as follows:
For the circumcenter
 and for the orthocenter
and for the orthocenter 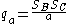

Hence:
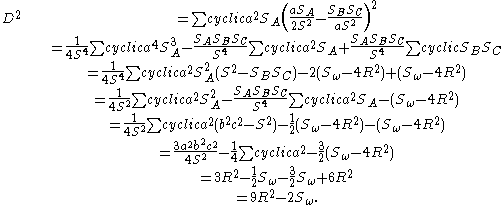
This gives: