
Convolution of probability distributions
Encyclopedia
The convolution of probability distributions arises in probability theory
and statistics
as the operation in terms of probability distribution
s that corresponds to the addition of independent random variable
s and, by extension, to forming linear combinations of random variables. The operation here is a special case of convolution
for which special results apply because the context is that of probability distributions.
of the sum of two or more independent random variable
s is the convolution of their individual distributions. The term is motivated by the fact that the probability mass function
or probability density function
of a sum of random variables is the convolution
of their corresponding probability mass functions or probability density functions respectively. Many well known distributions have simple convolutions: see List of convolutions of probability distributions
. Such methods can also be useful in deriving properties of the resulting distribution, such as moments, even if an explicit formula for the distribution itself cannot be derived.
One of the straightforward techniques is to use characteristic functions
, which always exists and are unique to a given distribution.

To show this let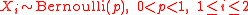
and define
Also, let Z denote a generic binomial random variable:
 are independent,
are independent,
Here, use was made of the fact that for k>n in the last but three equality, and of Pascal's rule in the second last equality.
for k>n in the last but three equality, and of Pascal's rule in the second last equality.
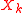 and of
and of  is
is
where t is within some neighborhood of zero.
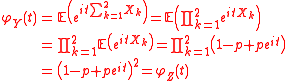
The expectation
of the product is the product of the expectations since each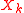 is independent.
is independent.
Since and
and  have the same characteristic function, they must have the same distribution.
have the same characteristic function, they must have the same distribution.
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
and statistics
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
as the operation in terms of probability distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
s that corresponds to the addition of independent random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
s and, by extension, to forming linear combinations of random variables. The operation here is a special case of convolution
Convolution
In mathematics and, in particular, functional analysis, convolution is a mathematical operation on two functions f and g, producing a third function that is typically viewed as a modified version of one of the original functions. Convolution is similar to cross-correlation...
for which special results apply because the context is that of probability distributions.
Introduction
The probability distributionProbability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
of the sum of two or more independent random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
s is the convolution of their individual distributions. The term is motivated by the fact that the probability mass function
Probability mass function
In probability theory and statistics, a probability mass function is a function that gives the probability that a discrete random variable is exactly equal to some value...
or probability density function
Probability density function
In probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
of a sum of random variables is the convolution
Convolution
In mathematics and, in particular, functional analysis, convolution is a mathematical operation on two functions f and g, producing a third function that is typically viewed as a modified version of one of the original functions. Convolution is similar to cross-correlation...
of their corresponding probability mass functions or probability density functions respectively. Many well known distributions have simple convolutions: see List of convolutions of probability distributions
Example derivation
There are several ways of derive formulae for the convolution of probability distributions. Often the manipulation of integrals can be avoided by use of some type of generating functionGenerating function
In mathematics, a generating function is a formal power series in one indeterminate, whose coefficients encode information about a sequence of numbers an that is indexed by the natural numbers. Generating functions were first introduced by Abraham de Moivre in 1730, in order to solve the general...
. Such methods can also be useful in deriving properties of the resulting distribution, such as moments, even if an explicit formula for the distribution itself cannot be derived.
One of the straightforward techniques is to use characteristic functions
Characteristic function (probability theory)
In probability theory and statistics, the characteristic function of any random variable completely defines its probability distribution. Thus it provides the basis of an alternative route to analytical results compared with working directly with probability density functions or cumulative...
, which always exists and are unique to a given distribution.
Convolution of Bernoulli distributions
The convolution of two independent Bernoulli random variables is a Binomial random variable. That is, in a shorthand notation,
To show this let
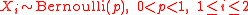
and define

Also, let Z denote a generic binomial random variable:

Using probability mass functions
As are independent,
are independent,
Here, use was made of the fact that
 for k>n in the last but three equality, and of Pascal's rule in the second last equality.
for k>n in the last but three equality, and of Pascal's rule in the second last equality.Using characteristic functions
The moment generating function of each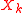 and of
and of  is
is
where t is within some neighborhood of zero.
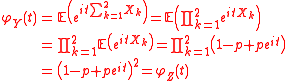
The expectation
Expected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
of the product is the product of the expectations since each
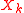 is independent.
is independent.Since
 and
and  have the same characteristic function, they must have the same distribution.
have the same characteristic function, they must have the same distribution.

