
Control variate
Encyclopedia
The control variates method is a variance reduction
technique used in Monte Carlo methods. It exploits information about the errors in estimates of known quantities to reduce the error of an estimate of an unknown quantity.
 , and assume we have a statistic
, and assume we have a statistic  such that
such that 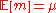 . Suppose we calculate another statistic
. Suppose we calculate another statistic  such that
such that  is a known value. Then
is a known value. Then

is also an unbiased estimator
for for any choice of the coefficient
for any choice of the coefficient  .
.
The variance
of the resulting estimator is
is
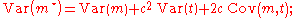
It can be shown that choosing the optimal coefficient
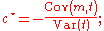
minimizes the variance of , and that with this choice,
, and that with this choice,
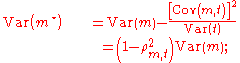
where
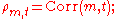
hence, the term variance reduction
. The greater the value of , the greater the variance reduction achieved.
, the greater the variance reduction achieved.
In the case that ,
,  , and/or
, and/or  are unknown, they can be estimated across the Monte Carlo replicates. This is equivalent to solving a certain least squares
are unknown, they can be estimated across the Monte Carlo replicates. This is equivalent to solving a certain least squares
system; therefore this technique is also known as regression sampling.
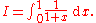
The exact result is . Using Monte Carlo integration, this integral can be seen as the expected value of
. Using Monte Carlo integration, this integral can be seen as the expected value of 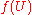 , where
, where

and U follows a uniform distribution
[0, 1].
Using a sample of size n denote the points in the sample as . Then the estimate is given by
. Then the estimate is given by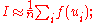
If we introduce as a control variate with a known expected value
as a control variate with a known expected value 
Using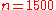 realizations and an estimated optimal coefficient
realizations and an estimated optimal coefficient  we obtain the following results
we obtain the following results
The variance was significantly reduced after using the control variates technique.
Variance reduction
In mathematics, more specifically in the theory of Monte Carlo methods, variance reduction is a procedure used to increase the precision of the estimates that can be obtained for a given number of iterations. Every output random variable from the simulation is associated with a variance which...
technique used in Monte Carlo methods. It exploits information about the errors in estimates of known quantities to reduce the error of an estimate of an unknown quantity.
Underlying principle
Let the parameter of interest be , and assume we have a statistic
, and assume we have a statistic  such that
such that 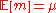 . Suppose we calculate another statistic
. Suppose we calculate another statistic  such that
such that  is a known value. Then
is a known value. Then
is also an unbiased estimator
Bias of an estimator
In statistics, bias of an estimator is the difference between this estimator's expected value and the true value of the parameter being estimated. An estimator or decision rule with zero bias is called unbiased. Otherwise the estimator is said to be biased.In ordinary English, the term bias is...
for
 for any choice of the coefficient
for any choice of the coefficient  .
.The variance
Variance
In probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
of the resulting estimator
 is
is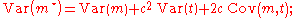
It can be shown that choosing the optimal coefficient
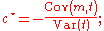
minimizes the variance of
 , and that with this choice,
, and that with this choice,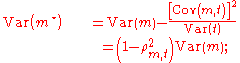
where
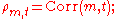
hence, the term variance reduction
Variance reduction
In mathematics, more specifically in the theory of Monte Carlo methods, variance reduction is a procedure used to increase the precision of the estimates that can be obtained for a given number of iterations. Every output random variable from the simulation is associated with a variance which...
. The greater the value of
 , the greater the variance reduction achieved.
, the greater the variance reduction achieved.In the case that
 ,
,  , and/or
, and/or  are unknown, they can be estimated across the Monte Carlo replicates. This is equivalent to solving a certain least squares
are unknown, they can be estimated across the Monte Carlo replicates. This is equivalent to solving a certain least squaresLeast squares
The method of least squares is a standard approach to the approximate solution of overdetermined systems, i.e., sets of equations in which there are more equations than unknowns. "Least squares" means that the overall solution minimizes the sum of the squares of the errors made in solving every...
system; therefore this technique is also known as regression sampling.
Example
We would like to estimate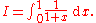
The exact result is
 . Using Monte Carlo integration, this integral can be seen as the expected value of
. Using Monte Carlo integration, this integral can be seen as the expected value of 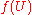 , where
, where
and U follows a uniform distribution
Uniform distribution (continuous)
In probability theory and statistics, the continuous uniform distribution or rectangular distribution is a family of probability distributions such that for each member of the family, all intervals of the same length on the distribution's support are equally probable. The support is defined by...
[0, 1].
Using a sample of size n denote the points in the sample as
 . Then the estimate is given by
. Then the estimate is given by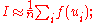
If we introduce
 as a control variate with a known expected value
as a control variate with a known expected value 
Using
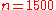 realizations and an estimated optimal coefficient
realizations and an estimated optimal coefficient  we obtain the following results
we obtain the following results| Estimate | Variance | |
| Classical estimate | 0.69475 | 0.01947 |
| Control variates | 0.69295 | 0.00060 |
The variance was significantly reduced after using the control variates technique.

