Constant-weight code
Encyclopedia
In coding theory
, a constant-weight code, also called an m of n code, is an error detection and correction
code where all codewords share the same Hamming weight
. The theory is closely connected to that of designs
(such as t-designs and Steiner system
s). Most of the work on this very vital field of discrete mathematics
is concerned with binary constant-weight codes.
Binary constant-weight codes have several applications, including frequency hopping
in GSM
networks.
Most barcode
s use a binary constant-weight code to simplify automatically setting the threshold.
In addition to use as error correction codes, the large space between code words can also be used in the design of asynchronous circuit
s such as delay insensitive circuit
s.
Constant-weight codes, like Berger code
s, can detect all unidirectional errors.
, Hamming distance
, and weight 
? This number is called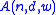 
.
Apart from some trivial observations, it is generally impossible to compute these numbers in a straightforward way. Upper bounds are given by several important theorems such as the first and second Johnson bounds, and better upper bounds can sometimes be found in other ways. Lower bounds are most often found by exhibiting specific codes, either with use of a variety of methods from discrete mathematics, or through heavy computer searching. A large table of such record-breaking codes was published in 1990, and an extension to longer codes (but only for those values of
and 
which are relevant for the GSM application) was published in 2006.
bits in a code-word of 
bits. The one-of-two code uses the code words 01 and 10 to encode the bits '0' and '1'. a one-of-four code can use the words 0001, 0010, 0100, 1000 in order to encode two bits 00, 01, 10, and 11. An example is dual rail encoding, and chain link used in delay insensitive circuits.
used by the United States Postal Service
.
The simplest implementation is to append a string of ones to the original data until it contains m ones, then append zeros to create a code of length n.
Example:
Coding theory
Coding theory is the study of the properties of codes and their fitness for a specific application. Codes are used for data compression, cryptography, error-correction and more recently also for network coding...
, a constant-weight code, also called an m of n code, is an error detection and correction
Error detection and correction
In information theory and coding theory with applications in computer science and telecommunication, error detection and correction or error control are techniques that enable reliable delivery of digital data over unreliable communication channels...
code where all codewords share the same Hamming weight
Hamming weight
The Hamming weight of a string is the number of symbols that are different from the zero-symbol of the alphabet used. It is thus equivalent to the Hamming distance from the all-zero string of the same length. For the most typical case, a string of bits, this is the number of 1's in the string...
. The theory is closely connected to that of designs
Combinatorial design
Combinatorial design theory is the part of combinatorial mathematics that deals with the existence and construction of systems of finite sets whose intersections have specified numerical properties....
(such as t-designs and Steiner system
Steiner system
250px|right|thumbnail|The [[Fano plane]] is an S Steiner triple system. The blocks are the 7 lines, each containing 3 points. Every pair of points belongs to a unique line....
s). Most of the work on this very vital field of discrete mathematics
Discrete mathematics
Discrete mathematics is the study of mathematical structures that are fundamentally discrete rather than continuous. In contrast to real numbers that have the property of varying "smoothly", the objects studied in discrete mathematics – such as integers, graphs, and statements in logic – do not...
is concerned with binary constant-weight codes.
Binary constant-weight codes have several applications, including frequency hopping
Frequency-hopping spread spectrum
Frequency-hopping spread spectrum is a method of transmitting radio signals by rapidly switching a carrier among many frequency channels, using a pseudorandom sequence known to both transmitter and receiver...
in GSM
Global System for Mobile Communications
GSM , is a standard set developed by the European Telecommunications Standards Institute to describe technologies for second generation digital cellular networks...
networks.
Most barcode
Barcode
A barcode is an optical machine-readable representation of data, which shows data about the object to which it attaches. Originally barcodes represented data by varying the widths and spacings of parallel lines, and may be referred to as linear or 1 dimensional . Later they evolved into rectangles,...
s use a binary constant-weight code to simplify automatically setting the threshold.
In addition to use as error correction codes, the large space between code words can also be used in the design of asynchronous circuit
Asynchronous circuit
An asynchronous circuit is a circuit in which the parts are largely autonomous. They are not governed by a clock circuit or global clock signal, but instead need only wait for the signals that indicate completion of instructions and operations. These signals are specified by simple data transfer...
s such as delay insensitive circuit
Delay insensitive circuit
A delay insensitive circuit is a type of asynchronous circuit which performs a logic operation often within a computing processor chip. Instead of using clock signals or other global control signals, the sequencing of computation in delay insensitive circuit is determined by the data...
s.
Constant-weight codes, like Berger code
Berger code
In telecommunication, a Berger code is a unidirectional error detecting code, named after its inventor, J. M. Berger. Berger codes can detect all unidirectional errors. Unidirectional errors are errors that only flip ones into zeroes or only zeroes into ones, such as in asymmetric channels...
s, can detect all unidirectional errors.
A(n,d,w)
The central problem regarding constant-weight codes is the following: what is the maximum number of codewords in a binary constant-weight code with length, Hamming distanceHamming distance
In information theory, the Hamming distance between two strings of equal length is the number of positions at which the corresponding symbols are different...
, and weight ? This number is called 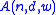.Apart from some trivial observations, it is generally impossible to compute these numbers in a straightforward way. Upper bounds are given by several important theorems such as the first and second Johnson bounds, and better upper bounds can sometimes be found in other ways. Lower bounds are most often found by exhibiting specific codes, either with use of a variety of methods from discrete mathematics, or through heavy computer searching. A large table of such record-breaking codes was published in 1990, and an extension to longer codes (but only for those values of
and which are relevant for the GSM application) was published in 2006.1 of N codes
A special case of constant weight codes are the one-of-N codes, that encode bits in a code-word of bits. The one-of-two code uses the code words 01 and 10 to encode the bits '0' and '1'. a one-of-four code can use the words 0001, 0010, 0100, 1000 in order to encode two bits 00, 01, 10, and 11. An example is dual rail encoding, and chain link used in delay insensitive circuits.m of n codes
An m of n code is a separable error detection code with a code word length of n bits, where each code word contains exactly m instances of a "one." A single bit error will cause the code word to have either m + 1 or m – 1 "ones." An example m-of-n code is the 2 of 5 codeTwo-out-of-five code
In telecommunication, a two-out-of-five code is an m of n code that provides exactly ten possible combinations, and thus is popular for representing decimal digits using five bits...
used by the United States Postal Service
United States Postal Service
The United States Postal Service is an independent agency of the United States government responsible for providing postal service in the United States...
.
The simplest implementation is to append a string of ones to the original data until it contains m ones, then append zeros to create a code of length n.
Example:
| Original 3 data bits | Appended bits |
|---|---|
| 000 | 111 |
| 001 | 110 |
| 010 | 110 |
| 011 | 100 |
| 100 | 110 |
| 101 | 100 |
| 110 | 100 |
| 111 | 000 |
External links
- Table of lower bounds on
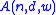maintained by Andries BrouwerAndries BrouwerAndries Evert Brouwer is a Dutch mathematician and computer programmer, a professor at Eindhoven University of Technology . His varied research interests include several branches of discrete mathematics, particularly graph theory and coding theory...
(update of the earlier table by Neil SloaneNeil SloaneNeil James Alexander Sloane is a British-U.S. mathematician. His major contributions are in the fields of combinatorics, error-correcting codes, and sphere packing...
and E. M. Rains) - Table of upper bounds on
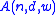maintained by Erik Agrell