Conditional quantifier
Encyclopedia
In logic
, a conditional quantifier is a kind of Lindström quantifier
(or generalized quantifier
)
that, relative to a classical model 
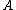, satisfies some or all of the following conditions ('X' and 'Y' range over arbitrary formulas in one free variable):
(The implication arrow denotes material implication in the metalanguage.) The minimal conditional logic M is characterized by the first six properties, and stronger conditional logics include some of the other ones. For example, the quantifier
, which can be viewed as set-theoretic inclusion, satisfies all of the above except [symmetry]. Clearly [symmetry] holds for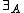 
while e.g. [contraposition] fails.
A semantic interpretation of conditional quantifiers involves a relation between sets of subsets of a given structure—i.e. a relation between properties defined on the structure. Some of the details can be found in the article Lindström quantifier
.
Conditional quantifiers are meant to capture certain properties concerning conditional reasoning at an abstract level. Generally, it is intended to clarify the role of conditionals in a first-order language as they relate to other connectives, such as conjunction or disjunction. While they can cover nested conditionals, the greater complexity of the formula, specifically the greater the number of conditional nesting, the less helpful they are as a methodological tool for understanding conditionals, at least in some sense. Compare this methodological strategy for conditionals with that of first-degree entailment
logics.
Logic
In philosophy, Logic is the formal systematic study of the principles of valid inference and correct reasoning. Logic is used in most intellectual activities, but is studied primarily in the disciplines of philosophy, mathematics, semantics, and computer science...
, a conditional quantifier is a kind of Lindström quantifier
Lindström quantifier
In mathematical logic, a Lindström quantifier is a generalized polyadic quantifier. They are a generalization of first-order quantifiers, such as the existential quantifier, the universal quantifier, and the counting quantifiers.They were introduced by Per Lindström in 1966.-Generalization of...
(or generalized quantifier
Generalized quantifier
In linguistic semantics, a generalized quantifier is an expression that denotes a property of a property, also called a higher-order property. This is the standard semantics assigned to quantified noun phrases, also called determiner phrases, in short: DP...
)
that, relative to a classical model 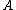, satisfies some or all of the following conditions ('X' and 'Y' range over arbitrary formulas in one free variable):
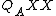[reflexivity]
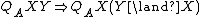[right conservativity]
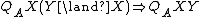[left conservativity]
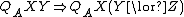[positive confirmation]
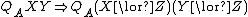[positive and negative confirmation]
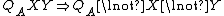[contraposition]
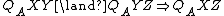[transitivity]
[weakening]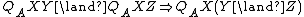
[conjunction]
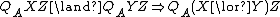[disjunction]
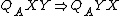[symmetry].
(The implication arrow denotes material implication in the metalanguage.) The minimal conditional logic M is characterized by the first six properties, and stronger conditional logics include some of the other ones. For example, the quantifier
, which can be viewed as set-theoretic inclusion, satisfies all of the above except [symmetry]. Clearly [symmetry] holds for 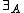while e.g. [contraposition] fails.A semantic interpretation of conditional quantifiers involves a relation between sets of subsets of a given structure—i.e. a relation between properties defined on the structure. Some of the details can be found in the article Lindström quantifier
Lindström quantifier
In mathematical logic, a Lindström quantifier is a generalized polyadic quantifier. They are a generalization of first-order quantifiers, such as the existential quantifier, the universal quantifier, and the counting quantifiers.They were introduced by Per Lindström in 1966.-Generalization of...
.
Conditional quantifiers are meant to capture certain properties concerning conditional reasoning at an abstract level. Generally, it is intended to clarify the role of conditionals in a first-order language as they relate to other connectives, such as conjunction or disjunction. While they can cover nested conditionals, the greater complexity of the formula, specifically the greater the number of conditional nesting, the less helpful they are as a methodological tool for understanding conditionals, at least in some sense. Compare this methodological strategy for conditionals with that of first-degree entailment
Paraconsistent logic
A paraconsistent logic is a logical system that attempts to deal with contradictions in a discriminating way. Alternatively, paraconsistent logic is the subfield of logic that is concerned with studying and developing paraconsistent systems of logic.Inconsistency-tolerant logics have been...
logics.