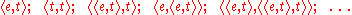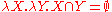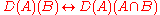Generalized quantifier
Encyclopedia
In linguistic
semantics
, a generalized quantifier is an expression that denotes a property
of a property, also called a higher-order property. This is the standard semantics assigned to quantified noun phrase
s, also called determiner phrase
s, in short: DP. The DP every boy below says of a property X that the set
of entities that are boys is a subset
of the set of entities that have property X. So the following sentence says that the set of boys is a subset of the set of sleepers.
This treatment of quantifiers has been essential in achieving a compositional semantics
for sentences containing quantifiers.
is often used to make the semantics of different kinds of expressions explicit. The standard construction defines the set of types recursively
as follows:
Given this definition, we have the simple types e and t, but also a countable infinity
of complex types, some of which include:
We can now assign types to the words in our sentence above (Every boy sleeps) as follows.
Thus, every denotes a function from a set to a function from a set to a truth value. Put differently, it denotes a function from a set to a set of sets. It is that function which for any two sets A,B, every(A)(B)= 1 if and only if
.
. For example, one can write the meaning of sleeps as the following lambda expression, which is a function from an individual x to the proposition that x sleeps.
Such lambda terms are functions whose domain is what precedes the period, and whose range are the type of thing that follows the period. If x is a variable that ranges over elements of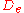
, then the following lambda term denotes the identity function
on individuals:
We can now write the meaning of every with the following lambda term, where X,Y are variables of type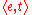
:
If we abbreviate the meaning of boy and sleeps as "B" and "S", respectively, we have that the sentence every boy sleeps now means the following:
The expression every is a determiner. Combined with a noun
, it yields a generalized quantifier of type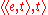
.
The GQ every boy is monotone increasing. For example, the set of things that run fast is a subset of the set of things that run. Therefore, the first sentence below entail
s the second:
just in case, for any two sets X and Y, the following holds:
An example of a monotone decreasing GQ is no boy. For this GQ we have that the first sentence below entails the second.
The lambda term for the determiner no is the following. It says that the two sets have an empty intersection
.
Monotone decreasing GQs are among the expressions that can license a negative polarity item, such as any. Monotone increasing GQs do not license negative polarity items.
The first sentence doesn't entail the second. The fact that the number of students that ran is exactly three doesn't entail that each of these students ran fast, so the number of students that did that can be smaller than 3. Conversely, the second sentence doesn't entail the first. The sentence exactly three students ran fast can be true, even though the number of students who merely ran (i.e. not so fast) is greater than 3.
The lambda term for the (complex) determiner exactly three is the following. It says that the cardinality of the intersection
between the two sets equals 3.
For example, the following two sentences are equivalent.
It has been proposed that all natural language determiners (i.e. in every language) are conservative (Barwise and Cooper 1981). The expression only is not conservative. The following two sentences are not equivalent. But it is, in fact not common to analyze only as a determiner. Rather, it is standardly treated as a focus-sensitive adverb
.
Linguistics
Linguistics is the scientific study of human language. Linguistics can be broadly broken into three categories or subfields of study: language form, language meaning, and language in context....
semantics
Semantics
Semantics is the study of meaning. It focuses on the relation between signifiers, such as words, phrases, signs and symbols, and what they stand for, their denotata....
, a generalized quantifier is an expression that denotes a property
Property (philosophy)
In modern philosophy, logic, and mathematics a property is an attribute of an object; a red object is said to have the property of redness. The property may be considered a form of object in its own right, able to possess other properties. A property however differs from individual objects in that...
of a property, also called a higher-order property. This is the standard semantics assigned to quantified noun phrase
Noun phrase
In grammar, a noun phrase, nominal phrase, or nominal group is a phrase based on a noun, pronoun, or other noun-like word optionally accompanied by modifiers such as adjectives....
s, also called determiner phrase
Determiner phrase
In linguistics, a determiner phrase is a syntactic category, a phrase headed by a determiner. The noun phrase is strictly speaking a determiner phrase, and NP designates a constituent of the noun phrase, taken to be the complement of the determiner. This is opposed to the traditional view that...
s, in short: DP. The DP every boy below says of a property X that the set
Set theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
of entities that are boys is a subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
of the set of entities that have property X. So the following sentence says that the set of boys is a subset of the set of sleepers.
-
- Every boy sleeps.
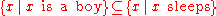
This treatment of quantifiers has been essential in achieving a compositional semantics
Semantics
Semantics is the study of meaning. It focuses on the relation between signifiers, such as words, phrases, signs and symbols, and what they stand for, their denotata....
for sentences containing quantifiers.
Type theory
A version of type theoryType theory
In mathematics, logic and computer science, type theory is any of several formal systems that can serve as alternatives to naive set theory, or the study of such formalisms in general...
is often used to make the semantics of different kinds of expressions explicit. The standard construction defines the set of types recursively
Recursion
Recursion is the process of repeating items in a self-similar way. For instance, when the surfaces of two mirrors are exactly parallel with each other the nested images that occur are a form of infinite recursion. The term has a variety of meanings specific to a variety of disciplines ranging from...
as follows:
- e and t are types.
- If a and b are both types, then so is
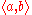
- Nothing is a type, except what can be constructed on the basis of lines 1 and 2 above.
Given this definition, we have the simple types e and t, but also a countable infinity
Infinity
Infinity is a concept in many fields, most predominantly mathematics and physics, that refers to a quantity without bound or end. People have developed various ideas throughout history about the nature of infinity...
of complex types, some of which include:
- Expressions of type e denote elements of the universe of discourse, the set of entities the discourse is about. This set is usually written as
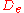. Examples of type e expressions include John and he. - Expressions of type t denote a truth value, usually rendered as the set
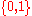, where 0 stands for "false" and 1 stands for "true". Examples of expressions that are sometimes said to be of type t are sentences or propositions. - Expressions of type
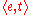denote functionsFunction (mathematics)In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
from the set of entities to the set of truth values. This set of functions is rendered as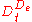
. Such functions are characteristic functionCharacteristic functionIn mathematics, characteristic function can refer to any of several distinct concepts:* The most common and universal usage is as a synonym for indicator function, that is the function* In probability theory, the characteristic function of any probability distribution on the real line is given by...
s of sets. They map every individual that is an element of the set to "true", and everything else to "false." It is common to say that they denote sets rather than characteristic functions, although, strictly speaking, the latter is more accurate. Examples of expressions of this type are predicatesPredicate (grammar)There are two competing notions of the predicate in theories of grammar. Traditional grammar tends to view a predicate as one of two main parts of a sentence, the other being the subject, which the predicate modifies. The other understanding of predicates is inspired from work in predicate calculus...
, nounNounIn linguistics, a noun is a member of a large, open lexical category whose members can occur as the main word in the subject of a clause, the object of a verb, or the object of a preposition .Lexical categories are defined in terms of how their members combine with other kinds of...
s and some kinds of adjectiveAdjectiveIn grammar, an adjective is a 'describing' word; the main syntactic role of which is to qualify a noun or noun phrase, giving more information about the object signified....
s. - In general, expressions of complex types
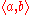denote functions from the set of entities of type 
to the set of entities of type 
, a construct we can write as follows: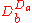 
.
We can now assign types to the words in our sentence above (Every boy sleeps) as follows.
-
- Type(boy)=
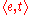
- Type(sleeps)=
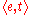
- Type(every)=
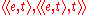
- Type(boy)=
Thus, every denotes a function from a set to a function from a set to a truth value. Put differently, it denotes a function from a set to a set of sets. It is that function which for any two sets A,B, every(A)(B)= 1 if and only if
.The typed lambda calculus
A useful way to write complex functions is the lambda calculusLambda calculus
In mathematical logic and computer science, lambda calculus, also written as λ-calculus, is a formal system for function definition, function application and recursion. The portion of lambda calculus relevant to computation is now called the untyped lambda calculus...
. For example, one can write the meaning of sleeps as the following lambda expression, which is a function from an individual x to the proposition that x sleeps.
Such lambda terms are functions whose domain is what precedes the period, and whose range are the type of thing that follows the period. If x is a variable that ranges over elements of
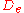, then the following lambda term denotes the identity functionIdentity function
In mathematics, an identity function, also called identity map or identity transformation, is a function that always returns the same value that was used as its argument...
on individuals:
We can now write the meaning of every with the following lambda term, where X,Y are variables of type
:
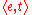If we abbreviate the meaning of boy and sleeps as "B" and "S", respectively, we have that the sentence every boy sleeps now means the following:
-
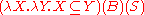— β-reduction
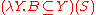— β-reduction
The expression every is a determiner. Combined with a noun
Noun
In linguistics, a noun is a member of a large, open lexical category whose members can occur as the main word in the subject of a clause, the object of a verb, or the object of a preposition .Lexical categories are defined in terms of how their members combine with other kinds of...
, it yields a generalized quantifier of type
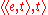.Monotone increasing GQs
A generalized quantifier GQ is said to be monotone increasing, also called upward entailing, just in case, for any two sets X and Y the following holds:-
- if
, then GQ(X) entailEntailmentIn logic, entailment is a relation between a set of sentences and a sentence. Let Γ be a set of one or more sentences; let S1 be the conjunction of the elements of Γ, and let S2 be a sentence: then, Γ entails S2 if and only if S1 and not-S2 are logically inconsistent...
s GQ(Y).
- if
The GQ every boy is monotone increasing. For example, the set of things that run fast is a subset of the set of things that run. Therefore, the first sentence below entail
Entailment
In logic, entailment is a relation between a set of sentences and a sentence. Let Γ be a set of one or more sentences; let S1 be the conjunction of the elements of Γ, and let S2 be a sentence: then, Γ entails S2 if and only if S1 and not-S2 are logically inconsistent...
s the second:
- Every boy runs fast.
- Every boy runs.
Monotone decreasing GQs
A GQ is said to be monotone decreasing, also called downward entailingDownward entailing
In linguistic semantics, a downward entailing expression is one that denotes a monotone decreasing function. A downward entailing expression reverses the relation of semantic strength among expressions. An expression like "run fast" is semantically stronger than the expression "run" since "run...
just in case, for any two sets X and Y, the following holds:
-
- If
, then GQ(Y) entails GQ(X).
- If
An example of a monotone decreasing GQ is no boy. For this GQ we have that the first sentence below entails the second.
- No boy runs.
- No boy runs fast.
The lambda term for the determiner no is the following. It says that the two sets have an empty intersection
Intersection (set theory)
In mathematics, the intersection of two sets A and B is the set that contains all elements of A that also belong to B , but no other elements....
.
Monotone decreasing GQs are among the expressions that can license a negative polarity item, such as any. Monotone increasing GQs do not license negative polarity items.
- Good: No boy has any money.
- Bad: *Every boy has any money.
Non-monotone GQs
A GQ is said to be non-monotone if it is neither monotone increasing nor monotone decreasing. An example of such a GQ is exactly three boys. Neither of the following two sentences entail the other.- Exactly three students ran.
- Exactly three students ran fast.
The first sentence doesn't entail the second. The fact that the number of students that ran is exactly three doesn't entail that each of these students ran fast, so the number of students that did that can be smaller than 3. Conversely, the second sentence doesn't entail the first. The sentence exactly three students ran fast can be true, even though the number of students who merely ran (i.e. not so fast) is greater than 3.
The lambda term for the (complex) determiner exactly three is the following. It says that the cardinality of the intersection
Intersection (set theory)
In mathematics, the intersection of two sets A and B is the set that contains all elements of A that also belong to B , but no other elements....
between the two sets equals 3.
Conservativity
A determiner D is said to be conservative if the following equivalence holds:
For example, the following two sentences are equivalent.
- Every boy sleeps.
- Every boy is a boy who sleeps.
It has been proposed that all natural language determiners (i.e. in every language) are conservative (Barwise and Cooper 1981). The expression only is not conservative. The following two sentences are not equivalent. But it is, in fact not common to analyze only as a determiner. Rather, it is standardly treated as a focus-sensitive adverb
Adverb
An adverb is a part of speech that modifies verbs or any part of speech other than a noun . Adverbs can modify verbs, adjectives , clauses, sentences, and other adverbs....
.
- Only boys sleep.
- Only boys are boys who sleep.