
Computation history
Encyclopedia
In computer science
, a computation history is a sequence of steps taken by an abstract machine
in the process of computing its result. Computation histories are frequently used in proofs
about the capabilities of certain machines, and particularly about the undecidability of various formal languages.
Formally, a computation history is a (normally finite) sequence of configurations of a formal automaton
. Each configuration fully describes the status of the machine at a particular point. To be valid, certain conditions must hold:
In addition, to be complete, a computation history must be finite and
The definitions of "valid initial configuration", "valid transition", and "valid terminal configuration" vary for different kinds of formal machines.
A deterministic automaton has exactly one computation history for a given initial configuration, though the history may be infinite and therefore incomplete.
 , a configuration is simply
, a configuration is simply
the current state of the machine, together with the remaining input. The first configuration must be the initial state of and the complete input. A transition from a configuration
and the complete input. A transition from a configuration  to
to
a configuration is allowed if
is allowed if  for
for
some input symbol and if
and if  has a transition from
has a transition from
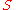 to
to  on input
on input  . The final
. The final
configuration must have the empty string as its remaining
as its remaining
input; whether has accepted or rejected the input depends
has accepted or rejected the input depends
on whether the final state is an accepting state.

where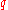 is the current state of the machine, represented in some
is the current state of the machine, represented in some
way that's distinguishable from the tape language, and where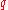 is
is
positioned immediately before the position of the read/write head.
Consider a Turing machine on input
on input  . The first
. The first
configuration must be , where
, where 
is the initial state of the Turing machine. The machine's state in the final
configuration must be either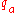 (the accept state) or
(the accept state) or 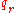
(the reject state). A configuration is a valid successor
is a valid successor
to configuration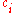 if there's a transition from the state in
if there's a transition from the state in
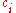 to the state in
to the state in  which manipulates the
which manipulates the
tape and moves the read/write head in a way that produces the result in
 .
.
pushdown automata are undecidable
. This is because the language of
non-accepting computation histories of a Turing machine
on input is a context-free language
is a context-free language
recognizable by a
non-deterministic pushdown automaton.
We encode a Turing computation history as the
as the
string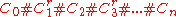 , where
, where 
is the encoding of configuration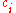 , as discussed above, and where
, as discussed above, and where
every other configuration is written in reverse. Before reading a particular
configuration, the pushdown automaton makes a non-deterministic choice
to either ignore the configuration or read it completely onto the stack.
In addition, the automaton verifies that the first configuration is the correct
initial configuration (if not, it accepts) and that the state of the final
configuration of the history is the accept state (if not, it accepts). Since
a non-deterministic automaton accepts if there's any valid way for it to accept,
the automaton described here will discover if the history is not a valid
accepting history and will accept if so, and reject if not.
This same trick cannot be used to recognize accepting computation histories
with an NPDA, since non-determinism could be used to skip past a test that would
otherwise fail. A linear-bounded Turing machine is sufficient to recognize
accepting computation histories.
This result allows us to prove that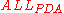 , the language
, the language
of pushdown automata which accept all input, is undecidable. Suppose
we have a decider for it, . For any Turing machine
. For any Turing machine
 and input
and input  , we can form the pushdown automaton
, we can form the pushdown automaton
 which accepts non-accepting computation histories for that
which accepts non-accepting computation histories for that
machine.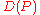 will accept if and only if there are no
will accept if and only if there are no
accepting computation histories for on
on  ; this
; this
would allow us to decide , which we know to be undecidable.
, which we know to be undecidable.
Computer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
, a computation history is a sequence of steps taken by an abstract machine
Abstract machine
An abstract machine, also called an abstract computer, is a theoretical model of a computer hardware or software system used in automata theory...
in the process of computing its result. Computation histories are frequently used in proofs
Mathematical proof
In mathematics, a proof is a convincing demonstration that some mathematical statement is necessarily true. Proofs are obtained from deductive reasoning, rather than from inductive or empirical arguments. That is, a proof must demonstrate that a statement is true in all cases, without a single...
about the capabilities of certain machines, and particularly about the undecidability of various formal languages.
Formally, a computation history is a (normally finite) sequence of configurations of a formal automaton
Automaton
An automaton is a self-operating machine. The word is sometimes used to describe a robot, more specifically an autonomous robot. An alternative spelling, now obsolete, is automation.-Etymology:...
. Each configuration fully describes the status of the machine at a particular point. To be valid, certain conditions must hold:
- the first configuration must be a valid initial configuration of the automaton and
- each transition between adjacent configurations must be valid according to the transition rules of the automaton.
In addition, to be complete, a computation history must be finite and
- the final configuration must be a valid terminal configuration of the automaton.
The definitions of "valid initial configuration", "valid transition", and "valid terminal configuration" vary for different kinds of formal machines.
A deterministic automaton has exactly one computation history for a given initial configuration, though the history may be infinite and therefore incomplete.
Finite State Machines
For a finite state machineFinite state machine
A finite-state machine or finite-state automaton , or simply a state machine, is a mathematical model used to design computer programs and digital logic circuits. It is conceived as an abstract machine that can be in one of a finite number of states...
 , a configuration is simply
, a configuration is simplythe current state of the machine, together with the remaining input. The first configuration must be the initial state of
 and the complete input. A transition from a configuration
and the complete input. A transition from a configuration  to
toa configuration
 is allowed if
is allowed if  for
forsome input symbol
 and if
and if  has a transition from
has a transition from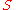 to
to  on input
on input  . The final
. The finalconfiguration must have the empty string
 as its remaining
as its remaininginput; whether
 has accepted or rejected the input depends
has accepted or rejected the input dependson whether the final state is an accepting state.
Turing Machines
Computation histories are more commonly used in reference to Turing machines. The configuration of a single-tape Turing machine consists of the contents of the tape, the position of the read/write head on the tape, and the current state of the associated state machine; this is usually written
where
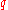 is the current state of the machine, represented in some
is the current state of the machine, represented in someway that's distinguishable from the tape language, and where
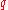 is
ispositioned immediately before the position of the read/write head.
Consider a Turing machine
 on input
on input  . The first
. The firstconfiguration must be
 , where
, where 
is the initial state of the Turing machine. The machine's state in the final
configuration must be either
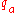 (the accept state) or
(the accept state) or 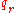
(the reject state). A configuration
 is a valid successor
is a valid successorto configuration
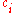 if there's a transition from the state in
if there's a transition from the state in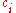 to the state in
to the state in  which manipulates the
which manipulates thetape and moves the read/write head in a way that produces the result in
 .
.Decidability results
Computation histories can be used to show that certain problems forpushdown automata are undecidable
Undecidable
Undecidable may refer to:In mathematics and logic* Undecidable problem - a decision problem which no algorithm can decide* "Undecidable" is sometimes used as a synonym of "independent", where a formula in mathematical logic is independent of a logical theory if neither that formula nor its negation...
. This is because the language of
non-accepting computation histories of a Turing machine

on input
 is a context-free language
is a context-free languageContext-free language
In formal language theory, a context-free language is a language generated by some context-free grammar. The set of all context-free languages is identical to the set of languages accepted by pushdown automata.-Examples:...
recognizable by a
non-deterministic pushdown automaton.
We encode a Turing computation history
 as the
as thestring
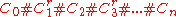 , where
, where 
is the encoding of configuration
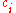 , as discussed above, and where
, as discussed above, and whereevery other configuration is written in reverse. Before reading a particular
configuration, the pushdown automaton makes a non-deterministic choice
to either ignore the configuration or read it completely onto the stack.
- If the pushdown automaton decides to ignore the configuration, it simply reads and discards it completely and makes the same choice for the next one.
- If it decides to process the configuration, it pushes it completely onto the stack, then verifies that the next configuration is a valid successor according to the rules of
 . Since successive configurations are always written in opposite orders, this can be done by, for each tape symbol in the new configuration, popping off a symbol from the stack and checking if they're the same. Where they disagree, it must be accountable for by a valid transition of
. Since successive configurations are always written in opposite orders, this can be done by, for each tape symbol in the new configuration, popping off a symbol from the stack and checking if they're the same. Where they disagree, it must be accountable for by a valid transition of  . If, at any point, the automaton decides that the transition is invalid, it immediately enters a special accept state which ignores the rest of the input and accepts at the end.
. If, at any point, the automaton decides that the transition is invalid, it immediately enters a special accept state which ignores the rest of the input and accepts at the end.
In addition, the automaton verifies that the first configuration is the correct
initial configuration (if not, it accepts) and that the state of the final
configuration of the history is the accept state (if not, it accepts). Since
a non-deterministic automaton accepts if there's any valid way for it to accept,
the automaton described here will discover if the history is not a valid
accepting history and will accept if so, and reject if not.
This same trick cannot be used to recognize accepting computation histories
with an NPDA, since non-determinism could be used to skip past a test that would
otherwise fail. A linear-bounded Turing machine is sufficient to recognize
accepting computation histories.
This result allows us to prove that
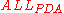 , the language
, the languageof pushdown automata which accept all input, is undecidable. Suppose
we have a decider for it,
 . For any Turing machine
. For any Turing machine and input
and input  , we can form the pushdown automaton
, we can form the pushdown automaton which accepts non-accepting computation histories for that
which accepts non-accepting computation histories for thatmachine.
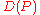 will accept if and only if there are no
will accept if and only if there are noaccepting computation histories for
 on
on  ; this
; thiswould allow us to decide
 , which we know to be undecidable.
, which we know to be undecidable.

