Complexity index
Encyclopedia
Besides complexity intended as a difficulty to compute a function (see computational complexity
), in modern computer science
and in statistics
another complexity index of a function stands for denoting its information content, in turn affecting the difficulty of learning the function from examples
.
Complexity indices in this sense characterize the entire class of functions to which the one we are interested in belongs. Focusing on Boolean functions, the detail of a class
of Boolean functions c essentially denotes how deeply the class is articulated.
To identify this index we must first define a sentry function of
.
Let us focus for a moment on a single function c, call it a concept defined on a set
of elements that we may figure as points in a Euclidean space
. In this framework, the above function associates to c a set of points that, since are defined to be external to the concept, prevent it from expanding into another function of
. We may dually define these points in terms of sentinelling a given concept c from being fully enclosed (invaded) by another concept within the class. Therefore we call these points either sentinels or sentry points; they are assigned by the sentry function 
to each concept of 
in such a way that:
The technical definition coming from is rooted in the inclusion of an augmented concept
made up of c plus its sentry points by another 
in the same class.
on a space 
, a sentry function is a total function 
satisfying the following conditions:
is the frontier of c upon 
.
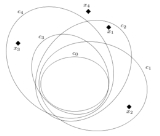
With reference to the picture on the right, 
is a candidate frontier of 
against 
. All points are in the gap between a 
and 
. They avoid inclusion of 
in 
, provided that these points are not used by the latter for sentineling itself against other concepts. Vice versa we expect that 
uses 
and 
as its own sentinels, 
uses 
and 
and 
uses 
and 
analogously. Point 
is not allowed as a 
sentry point since, like any diplomatic seat, it should be located outside all other concepts just to ensure that it is not occupied in case of invasion by 
.
,
is called detail of
. 
spans also over sentry functions on subsets of 
sentineling in this case the intersections of the concepts with these subsets. Actually, proper subsets of 
may host sentineling tasks that prove harder than those emerging with 
itself.
The detail
is a complexity measure of concept classes dual to the VC dimension
. The former uses points to separate sets of concepts, the latter concepts for partitioning sets of points. In particular the following inequality holds
See also Rademacher complexity
for a recently introduced class complexity index.
has detail 
, as shown in the picture on left below. Similarly, for the class of segments on 
, as shown in the picture on right.
on 
whose concepts are illustrated in the following scheme, where “
” denotes an element 
belonging to 
, “
” an element outside 
and 
a sentry point:
This class has
. As usual we may have different sentineling functions. A worst case 
, as illustrated, is: 
. However a cheaper one is 
:
Computational Complexity
Computational Complexity may refer to:*Computational complexity theory*Computational Complexity...
), in modern computer science
Computer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
and in statistics
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
another complexity index of a function stands for denoting its information content, in turn affecting the difficulty of learning the function from examples
Supervised learning
Supervised learning is the machine learning task of inferring a function from supervised training data. The training data consist of a set of training examples. In supervised learning, each example is a pair consisting of an input object and a desired output value...
.
Complexity indices in this sense characterize the entire class of functions to which the one we are interested in belongs. Focusing on Boolean functions, the detail of a class
of Boolean functions c essentially denotes how deeply the class is articulated.To identify this index we must first define a sentry function of
.Let us focus for a moment on a single function c, call it a concept defined on a set
of elements that we may figure as points in a Euclidean spaceEuclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
. In this framework, the above function associates to c a set of points that, since are defined to be external to the concept, prevent it from expanding into another function of
. We may dually define these points in terms of sentinelling a given concept c from being fully enclosed (invaded) by another concept within the class. Therefore we call these points either sentinels or sentry points; they are assigned by the sentry function to each concept of in such a way that:
- the sentry points are external to the concept c to be sentineled and internal to at least one other including it,
- each concept
including c has at least one of the sentry points of c either in the gap between c and 
, or outside 
and distinct from the sentry points of 
, and - they constitute a minimal set with these properties.
The technical definition coming from is rooted in the inclusion of an augmented concept
made up of c plus its sentry points by another in the same class.Definition of sentry function
For a concept class on a space , a sentry function is a total function satisfying the following conditions:
- Sentinels are outside the sentineled concept (
for all 
). - Sentinels are inside the invading concept (Having introduced the sets
, an invading concept 
is such that 
and 
. Denoting 
the set of concepts invading c, we must have that if 
, then 
). -
is a minimal set with the above properties (No 
exists satisfying (1) and (2) and having the property that 
for every 
). - Sentinels are honest guardians. It may be that
but 
so that 
. This however must be a consequence of the fact that all points of 
are involved in really sentineling c against other concepts in 
and not just in avoiding inclusion of 
by 
. Thus if we remove 
remains unchanged (Whenever 
and 
are such that 
and 
, then the restriction of 
to 
is a sentry function on this set).
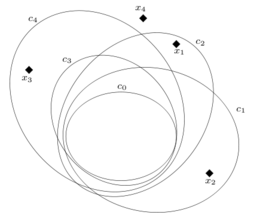
is the frontier of c upon . is a candidate frontier of against . All points are in the gap between a and . They avoid inclusion of in , provided that these points are not used by the latter for sentineling itself against other concepts. Vice versa we expect that uses and as its own sentinels, uses and and uses and analogously. Point is not allowed as a sentry point since, like any diplomatic seat, it should be located outside all other concepts just to ensure that it is not occupied in case of invasion by .Definition of detail
The frontier size of the most expensive concept to be sentineled with the least efficient sentineling function, i.e. the quantity,is called detail of
. spans also over sentry functions on subsets of sentineling in this case the intersections of the concepts with these subsets. Actually, proper subsets of may host sentineling tasks that prove harder than those emerging with itself.The detail
is a complexity measure of concept classes dual to the VC dimensionVC dimension
In statistical learning theory, or sometimes computational learning theory, the VC dimension is a measure of the capacity of a statistical classification algorithm, defined as the cardinality of the largest set of points that the algorithm can shatter...
. The former uses points to separate sets of concepts, the latter concepts for partitioning sets of points. In particular the following inequality holds See also Rademacher complexity
Rademacher complexity
In statistics and machine learning, Rademacher complexity, named after Hans Rademacher, measures richness of a class of real-valued functions with respect to a probability distribution....
for a recently introduced class complexity index.
Example: continuous spaces
Class C of circles in has detail , as shown in the picture on left below. Similarly, for the class of segments on , as shown in the picture on right.
 |
 |
Example: discrete spaces
The class on whose concepts are illustrated in the following scheme, where “” denotes an element belonging to , “” an element outside and a sentry point:  |
 |
 |
|
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
This class has
. As usual we may have different sentineling functions. A worst case , as illustrated, is: . However a cheaper one is :  |
 |
 |
|
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |