Rademacher complexity
Encyclopedia
In statistics
and machine learning
, Rademacher complexity, named after Hans Rademacher
, measures richness of a class of real-valued functions with respect to a probability distribution
.
Let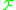
be a class of real-valued functions defined on a domain space 
.
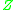The empirical Rademacher complexity of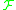
on a sample 
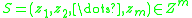is defined
as
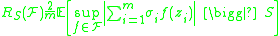
where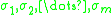
are independent random variables such that
for any 
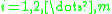. The random variables
are referred to as Rademacher variables.
Let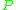
be a probability distribution over 
.
The Rademacher complexity of the function class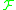
with respect to 
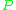for sample size 
is
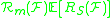
where the above expectation is taken over an identically independently distributed (i.i.d.) sample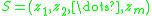
generated according to 
.
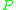One can show, for example, that there exists a constant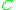
, such that any class of 
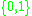-indicator functions with Vapnik-Chervonenkis dimension 
has Rademacher complexity upper-bounded by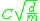 
.
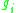instead of 
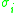, where 
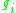are gaussian i.i.d.
random variables with zero-mean and variance 1, i.e.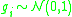
.
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
and machine learning
Machine learning
Machine learning, a branch of artificial intelligence, is a scientific discipline concerned with the design and development of algorithms that allow computers to evolve behaviors based on empirical data, such as from sensor data or databases...
, Rademacher complexity, named after Hans Rademacher
Hans Rademacher
Hans Adolph Rademacher was a German mathematician, known for work in mathematical analysis and number theory.-Biography:...
, measures richness of a class of real-valued functions with respect to a probability distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
.
Let
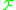be a class of real-valued functions defined on a domain space 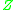.The empirical Rademacher complexity of
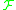on a sample 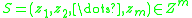is definedas
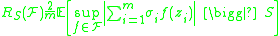
where
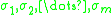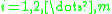are independent random variables such that for any . The random variables are referred to as Rademacher variables.Let
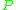be a probability distribution over .The Rademacher complexity of the function class
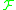with respect to 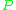for sample size is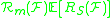where the above expectation is taken over an identically independently distributed (i.i.d.) sample
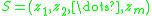generated according to 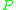.One can show, for example, that there exists a constant
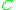, such that any class of 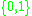-indicator functions with Vapnik-Chervonenkis dimension has Rademacher complexity upper-bounded by 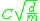.Gaussian complexity
Gaussian complexity is a similar complexity with similar physical meanings, and can be obtained from the previous complexity using the random variables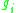 instead of 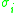, where 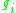are gaussian i.i.d.Independent and identically distributed random variables
In probability theory and statistics, a sequence or other collection of random variables is independent and identically distributed if each random variable has the same probability distribution as the others and all are mutually independent....
random variables with zero-mean and variance 1, i.e.
.
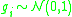