Complex wavelet transform
Encyclopedia
The complex wavelet transform (CWT) is a complex-valued extension to the standard discrete wavelet transform
(DWT). It is a two-dimensional wavelet
transform which provides multiresolution
, sparse representation, and useful characterization of the structure of an image. Further, it purveys a high degree of shift-invariance in its magnitude. However, a drawback to this transform is that it is exhibits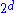
(where 
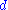is the dimension of the signal being transformed) redundancy compared to a separable (DWT).
The use of complex wavelets in image processing was originally set up in 1995 by J.M. Lina and L. Gagnon http://www.crim.ca/perso/langis.gagnon/articles/spie95.pdf in the framework of the Daubechies orthogonal filters bankshttp://portal.acm.org/citation.cfm?id=258030&dl=GUIDE&coll=GUIDE&CFID=10476702&CFTOKEN=44762573. It was then generalized in 1997 by Prof. Nick Kingsbury
of Cambridge University
.
In the area of computer vision, by exploiting the concept of visual contexts, one can quickly focus on candidate regions, where objects of interest may be found, and then compute additional features through the CWT for those regions only. These additional features, while not necessary for global regions, are useful in accurate detection and recognition of smaller objects. Similarly, the CWT may be applied to detect the activated voxels of cortex and additionally the temporal independent component analysis (tICA) may be utilized to extract the underlying independent sources whose number is determined by Bayesian information criterion http://www.springerlink.com/(t0ojvoayxrkdyk55vru2g245)/app/home/contribution.asp?referrer=parent&backto=issue,51,56;journal,180,3824;linkingpublicationresults,1:105633,1.
This redundancy of two provides extra information for analysis but at the expense of extra computational power. It also provides approximate shift-invariance (unlike the DWT) yet still allows perfect reconstruction of the signal.
The design of the filters is particularly important for the transform to occur correctly and the necessary characteristics are:
Discrete wavelet transform
In numerical analysis and functional analysis, a discrete wavelet transform is any wavelet transform for which the wavelets are discretely sampled...
(DWT). It is a two-dimensional wavelet
Wavelet
A wavelet is a wave-like oscillation with an amplitude that starts out at zero, increases, and then decreases back to zero. It can typically be visualized as a "brief oscillation" like one might see recorded by a seismograph or heart monitor. Generally, wavelets are purposefully crafted to have...
transform which provides multiresolution
Multiresolution analysis
A multiresolution analysis or multiscale approximation is the design method of most of the practically relevant discrete wavelet transforms and the justification for the algorithm of the fast wavelet transform...
, sparse representation, and useful characterization of the structure of an image. Further, it purveys a high degree of shift-invariance in its magnitude. However, a drawback to this transform is that it is exhibits
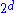(where 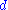is the dimension of the signal being transformed) redundancy compared to a separable (DWT).The use of complex wavelets in image processing was originally set up in 1995 by J.M. Lina and L. Gagnon http://www.crim.ca/perso/langis.gagnon/articles/spie95.pdf in the framework of the Daubechies orthogonal filters bankshttp://portal.acm.org/citation.cfm?id=258030&dl=GUIDE&coll=GUIDE&CFID=10476702&CFTOKEN=44762573. It was then generalized in 1997 by Prof. Nick Kingsbury
of Cambridge University
University of Cambridge
The University of Cambridge is a public research university located in Cambridge, United Kingdom. It is the second-oldest university in both the United Kingdom and the English-speaking world , and the seventh-oldest globally...
.
In the area of computer vision, by exploiting the concept of visual contexts, one can quickly focus on candidate regions, where objects of interest may be found, and then compute additional features through the CWT for those regions only. These additional features, while not necessary for global regions, are useful in accurate detection and recognition of smaller objects. Similarly, the CWT may be applied to detect the activated voxels of cortex and additionally the temporal independent component analysis (tICA) may be utilized to extract the underlying independent sources whose number is determined by Bayesian information criterion http://www.springerlink.com/(t0ojvoayxrkdyk55vru2g245)/app/home/contribution.asp?referrer=parent&backto=issue,51,56;journal,180,3824;linkingpublicationresults,1:105633,1.
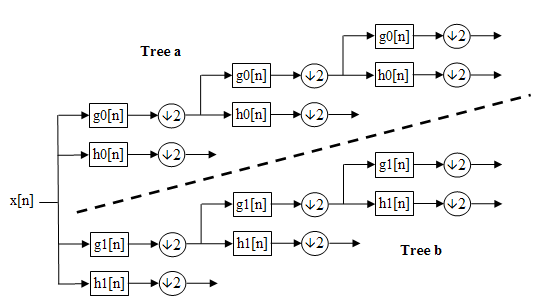
Dual-tree complex wavelet transform
The Dual-tree complex wavelet transform (DTCWT) calculates the complex transform of a signal using two separate DWT decompositions (tree a and tree b). If the filters used in one are specifically designed different from those in the other it is possible for one DWT to produce the real coefficients and the other the imaginary.The design of the filters is particularly important for the transform to occur correctly and the necessary characteristics are:
- The low-pass filterLow-pass filterA low-pass filter is an electronic filter that passes low-frequency signals but attenuates signals with frequencies higher than the cutoff frequency. The actual amount of attenuation for each frequency varies from filter to filter. It is sometimes called a high-cut filter, or treble cut filter...
s in the two trees must differ by half a sample period - Reconstruction filters are the reverse of analysis
- All filters from the same orthonormal set
- Tree a filters are the reverse of tree b filters
- Both trees have the same frequency response
External links
- An MPhil thesis: Complex wavelet transforms and their applications
- CWT for EMG analysis
- A paper on DTCWT
- Another full paper
- 3-D DT MRI data visualization
- A recent paper
- Image Analysis Using a Dual-Tree
-band Wavelet Transform (2006), preprint, Caroline Chaux, Laurent Duval, Jean-Christophe Pesquet - Noise covariance properties in dual-tree wavelet decompositions (2007), preprint, Caroline Chaux, Laurent Duval, Jean-Christophe Pesquet
- A nonlinear Stein based estimator for multichannel image denoising (2007), preprint, Caroline Chaux, Laurent Duval, Amel Benazza-Benyahia, Jean-Christophe Pesquet
- Caroline Chaux website (
-band dual-tree wavelets) - Laurent Duval website (
-band dual-tree wavelets) - James E. Fowler (dual-tree wavelets for video and hyperspectral image compression)
- Nick Kingsbury website (dual-tree wavelets)
- Jean-Christophe Pesquet website (
-band dual-tree wavelets) - Ivan Selesnick (dual-tree wavelets)