Complex beam parameter
Encyclopedia
In optics
, the complex beam parameter is a complex number
that specifies the properties of a Gaussian beam
at a particular point z along the axis of the beam. It is usually denoted by q. It can be calculated from the beam's vacuum wavelength
λ0, the radius of curvature
R of the phase front, the index of refraction n (n=1 for air), and the beam radius w (defined at 1/e2 intensity), according to: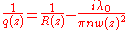
.
Alternatively, q can be calculated according to
where z is the location at which q is calculated, relative to the location of the beam waist, z0 is the Rayleigh range, and i is the imaginary unit
.
, which allows the calculation of the beam properties at any given point as it propagates through an optical system, if the ray matrix and the initial complex beam parameter is known. This same method can also be used to find the fundamental mode size of a stable optical resonator.
Given the initial beam parameter, qi, one can use the ray transfer matrix of an optical system,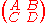
, to find the resulting beam parameter, qf, after the beam has traversed the system:
.
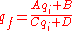It is often convenient to express this equation in terms of the reciprocals of q:
.
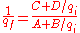To find the complex beam parameter of a stable optical resonator, one needs to find the ray matrix of the cavity. This is done by tracing the path of beam in the cavity. Assuming a starting point, find the matrix that goes through the cavity and return until the beam is in the same position and direction as the starting point. With this matrix and by making qi = qf, a quadratic is formed as:
.
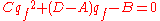Solving this equation gives the beam parameter for the chosen starting position in the cavity, and by propagating, the beam parameter for any other location in the cavity can be found.
Optics
Optics is the branch of physics which involves the behavior and properties of light, including its interactions with matter and the construction of instruments that use or detect it. Optics usually describes the behavior of visible, ultraviolet, and infrared light...
, the complex beam parameter is a complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
that specifies the properties of a Gaussian beam
Gaussian beam
In optics, a Gaussian beam is a beam of electromagnetic radiation whose transverse electric field and intensity distributions are well approximated by Gaussian functions. Many lasers emit beams that approximate a Gaussian profile, in which case the laser is said to be operating on the fundamental...
at a particular point z along the axis of the beam. It is usually denoted by q. It can be calculated from the beam's vacuum wavelength
Wavelength
In physics, the wavelength of a sinusoidal wave is the spatial period of the wave—the distance over which the wave's shape repeats.It is usually determined by considering the distance between consecutive corresponding points of the same phase, such as crests, troughs, or zero crossings, and is a...
λ0, the radius of curvature
Radius of curvature
The distance from the center of a circle or sphere to its surface is its radius. For other curved lines or surfaces, the radius of curvature at a given point is the radius of a circle that mathematically best fits the curve at that point....
R of the phase front, the index of refraction n (n=1 for air), and the beam radius w (defined at 1/e2 intensity), according to:
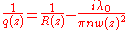.Alternatively, q can be calculated according to
where z is the location at which q is calculated, relative to the location of the beam waist, z0 is the Rayleigh range, and i is the imaginary unit
Imaginary unit
In mathematics, the imaginary unit allows the real number system ℝ to be extended to the complex number system ℂ, which in turn provides at least one root for every polynomial . The imaginary unit is denoted by , , or the Greek...
.
Uses of the complex beam parameter
The complex beam parameter is usually used in ray transfer matrix analysisRay transfer matrix analysis
Ray transfer matrix analysis is a type of ray tracing technique used in the design of some optical systems, particularly lasers...
, which allows the calculation of the beam properties at any given point as it propagates through an optical system, if the ray matrix and the initial complex beam parameter is known. This same method can also be used to find the fundamental mode size of a stable optical resonator.
Given the initial beam parameter, qi, one can use the ray transfer matrix of an optical system,
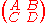, to find the resulting beam parameter, qf, after the beam has traversed the system: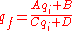.It is often convenient to express this equation in terms of the reciprocals of q:
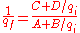.To find the complex beam parameter of a stable optical resonator, one needs to find the ray matrix of the cavity. This is done by tracing the path of beam in the cavity. Assuming a starting point, find the matrix that goes through the cavity and return until the beam is in the same position and direction as the starting point. With this matrix and by making qi = qf, a quadratic is formed as:
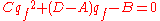.Solving this equation gives the beam parameter for the chosen starting position in the cavity, and by propagating, the beam parameter for any other location in the cavity can be found.