
Collectionwise normal
Encyclopedia
In mathematics
, a topological space
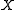 is called collectionwise normal if for every discrete family Fi (i ∈ I) of closed subsets of
is called collectionwise normal if for every discrete family Fi (i ∈ I) of closed subsets of  there exists a pairwise disjoint family of open sets Ui (i ∈ I), such that Fi ⊂ Ui. A family of subsets
there exists a pairwise disjoint family of open sets Ui (i ∈ I), such that Fi ⊂ Ui. A family of subsets 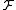 of subsets of
of subsets of 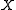 is called discrete when every point of
is called discrete when every point of 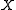 has a neighbourhood that intersects at most one of the sets from
has a neighbourhood that intersects at most one of the sets from 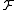 .
.
An equivalent definition demands that the above Ui (i ∈ I) are themselves a discrete family, which is stronger than pairwise disjoint.
Many authors assume that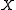 is also a T1 space as part of the definition.
is also a T1 space as part of the definition.
The property is intermediate in strength between paracompactness
and normality
, and occurs in metrisation theorems
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
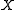 is called collectionwise normal if for every discrete family Fi (i ∈ I) of closed subsets of
is called collectionwise normal if for every discrete family Fi (i ∈ I) of closed subsets of  there exists a pairwise disjoint family of open sets Ui (i ∈ I), such that Fi ⊂ Ui. A family of subsets
there exists a pairwise disjoint family of open sets Ui (i ∈ I), such that Fi ⊂ Ui. A family of subsets 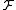 of subsets of
of subsets of 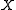 is called discrete when every point of
is called discrete when every point of 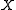 has a neighbourhood that intersects at most one of the sets from
has a neighbourhood that intersects at most one of the sets from 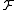 .
.An equivalent definition demands that the above Ui (i ∈ I) are themselves a discrete family, which is stronger than pairwise disjoint.
Many authors assume that
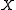 is also a T1 space as part of the definition.
is also a T1 space as part of the definition.The property is intermediate in strength between paracompactness
Paracompact space
In mathematics, a paracompact space is a topological space in which every open cover admits a locally finite open refinement. Paracompact spaces are sometimes also required to be Hausdorff. Paracompact spaces were introduced by ....
and normality
Normal space
In topology and related branches of mathematics, a normal space is a topological space X that satisfies Axiom T4: every two disjoint closed sets of X have disjoint open neighborhoods. A normal Hausdorff space is also called a T4 space...
, and occurs in metrisation theorems
Metrization theorem
In topology and related areas of mathematics, a metrizable space is a topological space that is homeomorphic to a metric space. That is, a topological space is said to be metrizable if there is a metricd\colon X \times X \to [0,\infty)...
.
Properties
- A collectionwise normal T1 space is collectionwise HausdorffCollectionwise Hausdorff spaceIn mathematics, in the field of topology, a topological space is said to be collectionwise Hausdorff if given any closed discrete collection of points in the topological space, there are pairwise disjoint open sets containing the points...
. - A collectionwise normal space is normalNormal spaceIn topology and related branches of mathematics, a normal space is a topological space X that satisfies Axiom T4: every two disjoint closed sets of X have disjoint open neighborhoods. A normal Hausdorff space is also called a T4 space...
. - A paracompact spaceParacompact spaceIn mathematics, a paracompact space is a topological space in which every open cover admits a locally finite open refinement. Paracompact spaces are sometimes also required to be Hausdorff. Paracompact spaces were introduced by ....
is collectionwise normal. - An Fσ-set in a collectionwise normal space is also collectionwise normal in the subspace topologySubspace topologyIn topology and related areas of mathematics, a subspace of a topological space X is a subset S of X which is equipped with a natural topology induced from that of X called the subspace topology .- Definition :Given a topological space and a subset S of X, the...
. In particular, this holds for closed subsets. - The Moore metrisation theorem states that a collectionwise normal Moore space is metrisable.

