Collaboration graph
Encyclopedia
In mathematics
and social science, a collaboration graph is a graph modeling some social network
where the vertices represent participants of that network (usually individual people) and where two distinct participants are joined by an edge whenever there is a collaborative relationship between them of a particular kind. Collaboration graphs are used to measure the closeness of collaborative relationships between the participants of the network.
Collaborations graphs have also been considered in other social networks, such as sports, including the "NBA graph" whose vertices are players where two players are joined by an edge if they have ever played together on the same team
The collaboration graph need not be connected. Thus people who never co-authored a joint paper represent isolated vertices in the collaboration graph of mathematicians.
Both the collaboration graph of mathematicians and movie actors were shown to have "small world topology": they have a very large number of vertices, most of small degree, that are highly clustered, and a "giant" connected component with small average distances between vertices.
The collaboration distance may be used, for instance, for evaluating the citations of an author, a group of authors or a journal .
In the collaboration graph of mathematicians, the collaboration distance from a particular person to Paul Erdős
is called the Erdős number
of that person. MathSciNet has a free online tool for computing the collaboration distance between any two mathematicians as well as the Erdős number of a mathematician. This tool also shows the actual chain of co-authors that realizes the collaboration distance.
For the Hollywood graph, an analog of the Erdős number, called the Bacon number, has also been considered, which measures the collaboration distance to Kevin Bacon
.
version, where individual mathematicians are vertices and where a group of mathematicians (not necessarily just two) constitutes a hyperedge if there is a paper that where they all were co-authors. Another variation is a simple graph where two mathematicians are joined by an edge if and only if there is a paper with only two of them (and no others) as co-authors.
A multigraph
version of a collaboration graph has also been considered where two mathematicians are joined by
edges if they co-authored exactly 
papers together. Another variation is a weighted collaboration graph where with rational weights where two mathematicians are joined by an edge with weight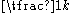 
whenever they co-authored exactly 
papers together. This model naturally leads to the notion of a "rational Erdős number".
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
and social science, a collaboration graph is a graph modeling some social network
Social network
A social network is a social structure made up of individuals called "nodes", which are tied by one or more specific types of interdependency, such as friendship, kinship, common interest, financial exchange, dislike, sexual relationships, or relationships of beliefs, knowledge or prestige.Social...
where the vertices represent participants of that network (usually individual people) and where two distinct participants are joined by an edge whenever there is a collaborative relationship between them of a particular kind. Collaboration graphs are used to measure the closeness of collaborative relationships between the participants of the network.
Types of collaboration graphs considered in the literature
The two most well-studied collaboration graphs are:- Collaboration graph of mathematicians also known as the Erdős collaboration graph, where two mathematicians are joined by an edge whenever they co-authored a paper together (with possibly other co-authors present).
- Collaboration graph of movie actors, also known as the Hollywood graph, where two movie actors are joined by an edge whenever they appeared in a movie together.
Collaborations graphs have also been considered in other social networks, such as sports, including the "NBA graph" whose vertices are players where two players are joined by an edge if they have ever played together on the same team
Features of collaboration graphs
By construction, the collaboration graph is a simple graph, since it has no loop-edges and no multiple edges.The collaboration graph need not be connected. Thus people who never co-authored a joint paper represent isolated vertices in the collaboration graph of mathematicians.
Both the collaboration graph of mathematicians and movie actors were shown to have "small world topology": they have a very large number of vertices, most of small degree, that are highly clustered, and a "giant" connected component with small average distances between vertices.
Collaboration distance
The distance between two people/nodes in a collaboration graph is called the collaboration distance. Thus the collaboration distance between two distinct nodes is equal to the smallest number of edges in an edge-path connecting them. If no path connecting two nodes in a collaboration graph exists, the collaboration distance between them is said to be infinite.The collaboration distance may be used, for instance, for evaluating the citations of an author, a group of authors or a journal .
In the collaboration graph of mathematicians, the collaboration distance from a particular person to Paul Erdős
Paul Erdos
Paul Erdős was a Hungarian mathematician. Erdős published more papers than any other mathematician in history, working with hundreds of collaborators. He worked on problems in combinatorics, graph theory, number theory, classical analysis, approximation theory, set theory, and probability theory...
is called the Erdős number
Erdos number
The Erdős number describes the "collaborative distance" between a person and mathematician Paul Erdős, as measured by authorship of mathematical papers.The same principle has been proposed for other eminent persons in other fields.- Overview :...
of that person. MathSciNet has a free online tool for computing the collaboration distance between any two mathematicians as well as the Erdős number of a mathematician. This tool also shows the actual chain of co-authors that realizes the collaboration distance.
For the Hollywood graph, an analog of the Erdős number, called the Bacon number, has also been considered, which measures the collaboration distance to Kevin Bacon
Kevin Bacon
Kevin Norwood Bacon is an American film and theater actor whose notable roles include Animal House, Diner, Footloose, Flatliners, Wild Things, A Few Good Men, JFK, Apollo 13, Mystic River, The Woodsman, Trapped, Friday the 13th, Hollow Man, Tremors, Death Sentence, Frost/Nixon, Crazy, Stupid, Love....
.
Generalizations of the collaboration graph
Some generalizations of the collaboration graph of mathematicians have also been considered. There is a hypergraphHypergraph
In mathematics, a hypergraph is a generalization of a graph, where an edge can connect any number of vertices. Formally, a hypergraph H is a pair H = where X is a set of elements, called nodes or vertices, and E is a set of non-empty subsets of X called hyperedges or links...
version, where individual mathematicians are vertices and where a group of mathematicians (not necessarily just two) constitutes a hyperedge if there is a paper that where they all were co-authors. Another variation is a simple graph where two mathematicians are joined by an edge if and only if there is a paper with only two of them (and no others) as co-authors.
A multigraph
Multigraph
In mathematics, a multigraph or pseudograph is a graph which is permitted to have multiple edges, , that is, edges that have the same end nodes. Thus two vertices may be connected by more than one edge....
version of a collaboration graph has also been considered where two mathematicians are joined by
edges if they co-authored exactly papers together. Another variation is a weighted collaboration graph where with rational weights where two mathematicians are joined by an edge with weight 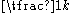whenever they co-authored exactly papers together. This model naturally leads to the notion of a "rational Erdős number".