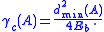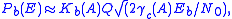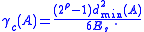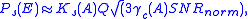Coding gain
Encyclopedia
In coding theory
and related engineering problems, coding gain is the measure in the difference between the signal to noise ratio (SNR) levels between the uncoded system and coded system required to reach the same bit error rate (BER) levels when used with the error correcting code (ECC).
 at the SNR level 4dB
at the SNR level 4dB
, and the corresponding coded (e.g., BCH
) system has the same BER at an SNR level of 2.5dB, then we say the coding gain = 4dB-2.5dB = 1.5dB, due to the code used (in this case BCH).
 [b/2D or b/s/Hz], i.e. the domain of binary signaling), the effective coding gain
[b/2D or b/s/Hz], i.e. the domain of binary signaling), the effective coding gain 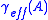 of a signal set
of a signal set  at a given target error probability per bit
at a given target error probability per bit 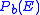 is defined as the difference in dB between the
is defined as the difference in dB between the 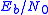 required to achieve the target
required to achieve the target 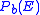 with
with  and the
and the 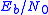 required to achieve the target
required to achieve the target 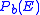 with 2-PAM
with 2-PAM
or (2×2)-QAM
(i.e. no coding). The nominal coding gain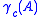 is defined as
is defined as
This definition is normalized so that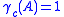 for 2-PAM or (2×2)-QAM. If the average number of nearest neighbors per transmitted bit
for 2-PAM or (2×2)-QAM. If the average number of nearest neighbors per transmitted bit 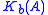 is equal to one, the effective coding gain
is equal to one, the effective coding gain  is approximately equal to the nominal coding gain
is approximately equal to the nominal coding gain 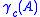 . However, if
. However, if 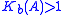 , the effective coding gain
, the effective coding gain 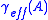 is less than the nominal coding gain
is less than the nominal coding gain  by an amount which depends on the steepness of the
by an amount which depends on the steepness of the 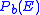 vs.
vs. 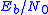 curve at the target
curve at the target 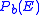 . This curve can be plotted using the union bound estimate (UBE)
. This curve can be plotted using the union bound estimate (UBE)
where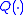 denotes the Gaussian probability of error function
denotes the Gaussian probability of error function
.
For the special case of a binary linear block code with parameters
with parameters 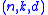 , the nominal spectral efficiency is
, the nominal spectral efficiency is  and the nominal coding gain is kd/n.
and the nominal coding gain is kd/n.
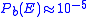 for Reed-Muller codes of length
for Reed-Muller codes of length  :
:
! Code !!  !!
!!  !!
!! 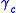 (dB) !!
(dB) !! 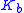 !!
!! 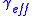 (dB)
(dB)
|-
| [8,7,2] > 1.75
7/4
2.43
4
| [8,4,4] 1.0
2
3.01
4
| [16,15,2] 1.88
15/8
2.73
8
| [16,11,4] 1.38
11/4
4.39
13
| [16,5,8] 0.63
5/2
3.98
6
| [32,31,2] 1.94
31/16
2.87
16
| [32,26,4] 1.63
13/4
5.12
48
| [32,16,8] 1.00
4
6.02
39
| [32,6,16] 0.37
3
4.77
10
| [64,63,2] 1.97
63/32
2.94
32
| [64,57,4] 1.78
57/16
5.52
183
| [64,42,8] 1.31
21/4
7.20
266
| [64,22,16] 0.69
11/2
7.40
118
| [64,7,32] 0.22
7/2
5.44
18
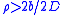 , i.e. the domain of non-binary signaling), the effective coding gain
, i.e. the domain of non-binary signaling), the effective coding gain 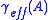 of a signal set
of a signal set  at a given target error rate
at a given target error rate 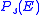 is defined as the difference in dB between the
is defined as the difference in dB between the 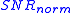 required to achieve the target
required to achieve the target 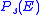 with
with  and the
and the 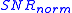 required to achieve the target
required to achieve the target 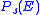 with M-PAM
with M-PAM
or (M×M)-QAM
(i.e. no coding). The nominal coding gain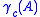 is defined as
is defined as
This definition is normalized so that for M-PAM or (M×M)-QAM. The UBE becomes
for M-PAM or (M×M)-QAM. The UBE becomes
where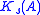 is the average number of nearest neighbors per two dimensions.
is the average number of nearest neighbors per two dimensions.
Coding theory
Coding theory is the study of the properties of codes and their fitness for a specific application. Codes are used for data compression, cryptography, error-correction and more recently also for network coding...
and related engineering problems, coding gain is the measure in the difference between the signal to noise ratio (SNR) levels between the uncoded system and coded system required to reach the same bit error rate (BER) levels when used with the error correcting code (ECC).
Example
If the uncoded BPSK system in AWGN environment has a Bit error rate (BER) of at the SNR level 4dB
at the SNR level 4dBDecibel
The decibel is a logarithmic unit that indicates the ratio of a physical quantity relative to a specified or implied reference level. A ratio in decibels is ten times the logarithm to base 10 of the ratio of two power quantities...
, and the corresponding coded (e.g., BCH
BCH code
In coding theory the BCH codes form a class of parameterised error-correcting codes which have been the subject of much academic attention in the last fifty years. BCH codes were invented in 1959 by Hocquenghem, and independently in 1960 by Bose and Ray-Chaudhuri...
) system has the same BER at an SNR level of 2.5dB, then we say the coding gain = 4dB-2.5dB = 1.5dB, due to the code used (in this case BCH).
Power-limited regime
In the power-limited regime (where the nominal spectral efficiencySpectral efficiency
Spectral efficiency, spectrum efficiency or bandwidth efficiency refers to the information rate that can be transmitted over a given bandwidth in a specific communication system...
 [b/2D or b/s/Hz], i.e. the domain of binary signaling), the effective coding gain
[b/2D or b/s/Hz], i.e. the domain of binary signaling), the effective coding gain 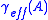 of a signal set
of a signal set  at a given target error probability per bit
at a given target error probability per bit 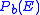 is defined as the difference in dB between the
is defined as the difference in dB between the 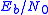 required to achieve the target
required to achieve the target 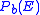 with
with  and the
and the 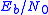 required to achieve the target
required to achieve the target 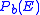 with 2-PAM
with 2-PAMPulse-amplitude modulation
Pulse-amplitude modulation, acronym PAM, is a form of signal modulation where the message information is encoded in the amplitude of a series of signal pulses....
or (2×2)-QAM
Quadrature amplitude modulation
Quadrature amplitude modulation is both an analog and a digital modulation scheme. It conveys two analog message signals, or two digital bit streams, by changing the amplitudes of two carrier waves, using the amplitude-shift keying digital modulation scheme or amplitude modulation analog...
(i.e. no coding). The nominal coding gain
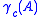 is defined as
is defined asThis definition is normalized so that
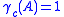 for 2-PAM or (2×2)-QAM. If the average number of nearest neighbors per transmitted bit
for 2-PAM or (2×2)-QAM. If the average number of nearest neighbors per transmitted bit 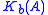 is equal to one, the effective coding gain
is equal to one, the effective coding gain  is approximately equal to the nominal coding gain
is approximately equal to the nominal coding gain 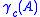 . However, if
. However, if 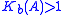 , the effective coding gain
, the effective coding gain 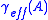 is less than the nominal coding gain
is less than the nominal coding gain  by an amount which depends on the steepness of the
by an amount which depends on the steepness of the 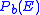 vs.
vs. 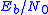 curve at the target
curve at the target 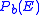 . This curve can be plotted using the union bound estimate (UBE)
. This curve can be plotted using the union bound estimate (UBE)where
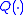 denotes the Gaussian probability of error function
denotes the Gaussian probability of error functionError function
In mathematics, the error function is a special function of sigmoid shape which occurs in probability, statistics and partial differential equations...
.
For the special case of a binary linear block code
 with parameters
with parameters 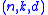 , the nominal spectral efficiency is
, the nominal spectral efficiency is  and the nominal coding gain is kd/n.
and the nominal coding gain is kd/n.Example
The table below lists the nominal spectral efficiency, nominal coding gain and effective coding gain at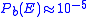 for Reed-Muller codes of length
for Reed-Muller codes of length  :
: !!
!!  !!
!! 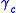 (dB) !!
(dB) !! 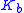 !!
!! 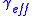 (dB)
(dB)|-
| [8,7,2] >
| [8,4,4]
| [16,15,2]
| [16,11,4]
| [16,5,8]
| [32,31,2]
| [32,26,4]
| [32,16,8]
| [32,6,16]
| [64,63,2]
| [64,57,4]
| [64,42,8]
| [64,22,16]
| [64,7,32]
Bandwidth-limited regime
In the bandwidth-limited regime (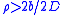 , i.e. the domain of non-binary signaling), the effective coding gain
, i.e. the domain of non-binary signaling), the effective coding gain 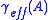 of a signal set
of a signal set  at a given target error rate
at a given target error rate 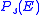 is defined as the difference in dB between the
is defined as the difference in dB between the 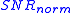 required to achieve the target
required to achieve the target 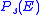 with
with  and the
and the 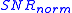 required to achieve the target
required to achieve the target 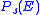 with M-PAM
with M-PAMPulse-amplitude modulation
Pulse-amplitude modulation, acronym PAM, is a form of signal modulation where the message information is encoded in the amplitude of a series of signal pulses....
or (M×M)-QAM
Quadrature amplitude modulation
Quadrature amplitude modulation is both an analog and a digital modulation scheme. It conveys two analog message signals, or two digital bit streams, by changing the amplitudes of two carrier waves, using the amplitude-shift keying digital modulation scheme or amplitude modulation analog...
(i.e. no coding). The nominal coding gain
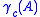 is defined as
is defined asThis definition is normalized so that
 for M-PAM or (M×M)-QAM. The UBE becomes
for M-PAM or (M×M)-QAM. The UBE becomeswhere
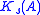 is the average number of nearest neighbors per two dimensions.
is the average number of nearest neighbors per two dimensions.