Chromatic circle
Encyclopedia
Chromatic scale
The chromatic scale is a musical scale with twelve pitches, each a semitone apart. On a modern piano or other equal-tempered instrument, all the half steps are the same size...
. If one starts on any equal-tempered pitch and repeatedly ascends by the musical interval of a semitone, one will eventually land on a pitch with the same pitch class
Pitch class
In music, a pitch class is a set of all pitches that are a whole number of octaves apart, e.g., the pitch class C consists of the Cs in all octaves...
as the initial one, passing through all the other equal-tempered chromatic pitch classes in between.
Since the space is circular, it is also possible to descend by semitone. The chromatic circle is useful because it represents melodic distance, which is often correlated with physical distance on musical instruments. For instance, to move from any C on a piano keyboard to the nearest E, one must move up four semitones, corresponding to four clockwise steps on the chromatic circle. One can also move down by eight semitones, corresponding to eight counterclockwise steps on the pitch class circle. Larger motions on the piano (or in pitch space
Pitch space
In music theory, pitch spaces model relationships between pitches. These models typically use distance to model the degree of relatedness, with closely related pitches placed near one another, and less closely related pitches placed farther apart. Depending on the complexity of the relationships...
) can be represented in pitch class space by paths that "wrap around" the chromatic circle one or more times.
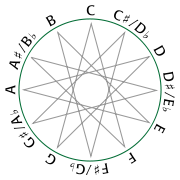
Circle of fifths
In music theory, the circle of fifths shows the relationships among the 12 tones of the chromatic scale, their corresponding key signatures, and the associated major and minor keys...
is that the former is truly a continuous space: every point on the circle corresponds to a conceivable pitch class
Pitch class
In music, a pitch class is a set of all pitches that are a whole number of octaves apart, e.g., the pitch class C consists of the Cs in all octaves...
, and every conceivable pitch class corresponds to a point on the circle. By contrast, the circle of fifths is fundamentally a discrete structure, and there is no obvious way to assign pitch classes to each of its points. A mathematician would say that the circle of fifths and the chromatic circle are not homeomorphic.
However, one can represent the twelve equal-tempered pitch classes by the cyclic group
Cyclic group
In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
of order twelve, or equivalently, the residue classes
Modular arithmetic
In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
modulo twelve, Z/12Z. The group
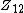has four generatorsGenerating set of a group
In abstract algebra, a generating set of a group is a subset that is not contained in any proper subgroup of the group. Equivalently, a generating set of a group is a subset such that every element of the group can be expressed as the combination of finitely many elements of the subset and their...
, which can be identified with the ascending and descending semitones and the ascending and descending perfect fifths. The semitonal generator gives rise to the chromatic circle while the perfect fifth gives rise to the circle of fifths
Circle of fifths
In music theory, the circle of fifths shows the relationships among the 12 tones of the chromatic scale, their corresponding key signatures, and the associated major and minor keys...
.