
Causality conditions
Encyclopedia
In the study of Lorentzian manifold spacetime
s there exists a hierarchy of causality conditions which are important in proving mathematical theorems about the global structure of such manifolds. These conditions were collected during the late 1970s.
The weaker the causality condition on a spacetime, the more unphysical the spacetime is. Spacetimes with closed timelike curve
s, for example, present severe interpretational difficulties. See the grandfather paradox
.
It is reasonable to believe that any physical spacetime will satisfy the strongest causality condition: global hyperbolicity. For such spacetimes the equations in general relativity
can be posed as an initial value problem
on a Cauchy surface
.
We now give definitions of these causality conditions for a Lorentzian manifold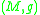 . Where two or more are given they are equivalent.
. Where two or more are given they are equivalent.
Notation:
(See causal structure for definitions.)
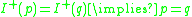
. A spacetime is stably causal if it cannot be made to contain closed causal curves by arbitrarily small perturbations of the metric. Stephen Hawking
showed that this is equivalent to:
Robert Geroch
showed that a spacetime is globally hyperbolic if and only if
there exists a Cauchy surface
for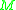 . This means that:
. This means that:
Spacetime
In physics, spacetime is any mathematical model that combines space and time into a single continuum. Spacetime is usually interpreted with space as being three-dimensional and time playing the role of a fourth dimension that is of a different sort from the spatial dimensions...
s there exists a hierarchy of causality conditions which are important in proving mathematical theorems about the global structure of such manifolds. These conditions were collected during the late 1970s.
The weaker the causality condition on a spacetime, the more unphysical the spacetime is. Spacetimes with closed timelike curve
Closed timelike curve
In mathematical physics, a closed timelike curve is a worldline in a Lorentzian manifold, of a material particle in spacetime that is "closed," returning to its starting point...
s, for example, present severe interpretational difficulties. See the grandfather paradox
Grandfather paradox
The grandfather paradox is a proposed paradox of time travel first described by the science fiction writer René Barjavel in his 1943 book Le Voyageur Imprudent . The paradox is this: suppose a man traveled back in time and killed his biological grandfather before the latter met the traveler's...
.
It is reasonable to believe that any physical spacetime will satisfy the strongest causality condition: global hyperbolicity. For such spacetimes the equations in general relativity
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
can be posed as an initial value problem
Initial value problem
In mathematics, in the field of differential equations, an initial value problem is an ordinary differential equation together with a specified value, called the initial condition, of the unknown function at a given point in the domain of the solution...
on a Cauchy surface
Cauchy surface
Intuitively, a Cauchy surface is a plane in space-time which is like an instant of time; its significance is that giving the initial conditions on this plane determines the future uniquely....
.
The hierarchy
There is a hierarchy of causality conditions, each one of which is strictly stronger than the previous. This is sometimes called the causal ladder. The conditions, from weakest to strongest, are:- Non-totally vicious
- Chronological
- Causal
- Distinguishing
- Strongly causal
- Stably causal
- Causally continuous
- Causally simple
- Globally hyperbolic
We now give definitions of these causality conditions for a Lorentzian manifold
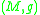 . Where two or more are given they are equivalent.
. Where two or more are given they are equivalent.Notation:
-
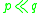 denotes the chronological relation.
denotes the chronological relation. -
 denotes the causal relation.
denotes the causal relation.
(See causal structure for definitions.)
Chronological
- There are no closed chronological (timelike) curves.
- The chronological relation is irreflexive:
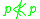 for all
for all  .
.
Causal
- There are no closed causal (non-spacelike) curves.
- If both
 and
and 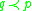 then
then 
Past-distinguishing
- Two points
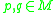 which share the same chronological past are the same point:
which share the same chronological past are the same point:
-
-

- For any neighborhood
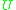 of
of 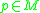 there exists a neighborhood
there exists a neighborhood 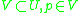 such that no past-directed non-spacelike curve from
such that no past-directed non-spacelike curve from 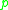 intersects
intersects 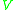 more than once.
more than once.
- For any neighborhood
-
Future-distinguishing
- Two points
 which share the same chronological future are the same point:
which share the same chronological future are the same point:
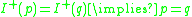
- For any neighborhood
 of
of 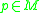 there exists a neighborhood
there exists a neighborhood  such that no future-directed non-spacelike curve from
such that no future-directed non-spacelike curve from 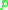 intersects
intersects 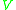 more than once.
more than once.
Strongly causal
- For any
 there exists a neighborhood
there exists a neighborhood  of
of 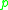 such that there exists no timelike curve that passes through
such that there exists no timelike curve that passes through 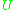 more than once.
more than once. - For any neighborhood
 of
of  there exists a neighborhood
there exists a neighborhood 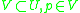 such that
such that 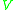 is causally convex in
is causally convex in 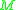 (and thus in
(and thus in 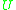 ).
). - The Alexandrov topologyAlexandrov topologyIn topology, an Alexandrov space is a topological space in which the intersection of any family of open sets is open. It is an axiom of topology that the intersection of any finite family of open sets is open...
agrees with the manifold topology.
Stably causal
A manifold satisfying any of the weaker causality conditions defined above may fail to do so if the metric is given a small perturbationPerturbation theory
Perturbation theory comprises mathematical methods that are used to find an approximate solution to a problem which cannot be solved exactly, by starting from the exact solution of a related problem...
. A spacetime is stably causal if it cannot be made to contain closed causal curves by arbitrarily small perturbations of the metric. Stephen Hawking
Stephen Hawking
Stephen William Hawking, CH, CBE, FRS, FRSA is an English theoretical physicist and cosmologist, whose scientific books and public appearances have made him an academic celebrity...
showed that this is equivalent to:
- There exists a global time function on
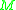 . This is a scalarScalar (physics)In physics, a scalar is a simple physical quantity that is not changed by coordinate system rotations or translations , or by Lorentz transformations or space-time translations . This is in contrast to a vector...
. This is a scalarScalar (physics)In physics, a scalar is a simple physical quantity that is not changed by coordinate system rotations or translations , or by Lorentz transformations or space-time translations . This is in contrast to a vector...
field on
on 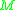 whose gradient
whose gradient  is everywhere timelike and future-directed. This global time function gives us a stable way to distinguish between future and past for each point of the spacetime (and so we have no causal violations).
is everywhere timelike and future-directed. This global time function gives us a stable way to distinguish between future and past for each point of the spacetime (and so we have no causal violations).
Globally hyperbolic
-
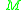 is strongly causal and every set
is strongly causal and every set 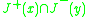 (for points
(for points  ) is compactCompact spaceIn mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
) is compactCompact spaceIn mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
.
Robert Geroch
Robert Geroch
Robert Geroch is a theoretical physicist and professor at the University of Chicago. He has worked prominently on general relativity and mathematical physics and has promoted the use of category theory in mathematics and physics. He was the Ph.D. supervisor for Abhay Ashtekar.Geroch obtained his Ph.D...
showed that a spacetime is globally hyperbolic if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
there exists a Cauchy surface
Cauchy surface
Intuitively, a Cauchy surface is a plane in space-time which is like an instant of time; its significance is that giving the initial conditions on this plane determines the future uniquely....
for
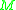 . This means that:
. This means that:
-
 is topologically equivalent to
is topologically equivalent to 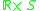 for some Cauchy surfaceCauchy surfaceIntuitively, a Cauchy surface is a plane in space-time which is like an instant of time; its significance is that giving the initial conditions on this plane determines the future uniquely....
for some Cauchy surfaceCauchy surfaceIntuitively, a Cauchy surface is a plane in space-time which is like an instant of time; its significance is that giving the initial conditions on this plane determines the future uniquely....
 (Here
(Here 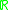 denotes the real lineReal lineIn mathematics, the real line, or real number line is the line whose points are the real numbers. That is, the real line is the set of all real numbers, viewed as a geometric space, namely the Euclidean space of dimension one...
denotes the real lineReal lineIn mathematics, the real line, or real number line is the line whose points are the real numbers. That is, the real line is the set of all real numbers, viewed as a geometric space, namely the Euclidean space of dimension one...
).
See also
- SpacetimeSpacetimeIn physics, spacetime is any mathematical model that combines space and time into a single continuum. Spacetime is usually interpreted with space as being three-dimensional and time playing the role of a fourth dimension that is of a different sort from the spatial dimensions...
- Lorentzian manifold
- Causal structureCausal structureIn mathematical physics, the causal structure of a Lorentzian manifold describes the causal relationships between points in the manifold.- Introduction :In modern physics spacetime is represented by a Lorentzian manifold...
- Globally hyperbolic manifold
- Closed timelike curveClosed timelike curveIn mathematical physics, a closed timelike curve is a worldline in a Lorentzian manifold, of a material particle in spacetime that is "closed," returning to its starting point...

