Carathéodory's existence theorem
Encyclopedia
In mathematics
, Carathéodory's existence theorem says that an ordinary differential equation
has a solution under relatively mild conditions. It is a generalization of Peano's existence theorem
. Peano's theorem requires that the right-hand side of the differential equation is continuous, while Carathéodory's theorem shows existence of solutions (in a more general sense) for some discontinuous equations. The theorem is named after Constantin Carathéodory
.
with initial condition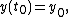
where the function ƒ is defined on a rectangular domain of the form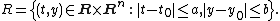
Peano's existence theorem states that if ƒ is continuous
, then the differential equation has at least one solution in a neighbourhood of the initial condition.
However, it is also possible to consider differential equations with a discontinuous right-hand side, like the equation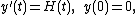
where H denotes the Heaviside function defined by
It makes sense to consider the ramp function
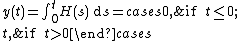
as a solution of the differential equation. Strictly speaking though, it does not satisfy the differential equation at
, because the function is not differentiable there. This suggests that the idea of a solution be extended to allow for solutions that are not everywhere differentiable, thus motivating the following definition.
A function y is called a solution in the extended sense of the differential equation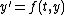
with initial condition 
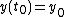if y is absolutely continuous
, y satisfies the differential equation almost everywhere
and y satisfies the initial condition. The absolute continuity of y implies that its derivative exists almost everywhere.
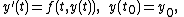
with ƒ on the rectangular domain R. If ƒ satisfies the three conditions
then the differential equation has a solution in the extended sense in a neighbourhood of the initial condition.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Carathéodory's existence theorem says that an ordinary differential equation
Ordinary differential equation
In mathematics, an ordinary differential equation is a relation that contains functions of only one independent variable, and one or more of their derivatives with respect to that variable....
has a solution under relatively mild conditions. It is a generalization of Peano's existence theorem
Peano existence theorem
In mathematics, specifically in the study of ordinary differential equations, the Peano existence theorem, Peano theorem or Cauchy-Peano theorem, named after Giuseppe Peano and Augustin Louis Cauchy, is a fundamental theorem which guarantees the existence of solutions to certain initial value...
. Peano's theorem requires that the right-hand side of the differential equation is continuous, while Carathéodory's theorem shows existence of solutions (in a more general sense) for some discontinuous equations. The theorem is named after Constantin Carathéodory
Constantin Carathéodory
Constantin Carathéodory was a Greek mathematician. He made significant contributions to the theory of functions of a real variable, the calculus of variations, and measure theory...
.
Introduction
Consider the differential equationwith initial condition
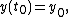
where the function ƒ is defined on a rectangular domain of the form
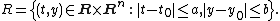
Peano's existence theorem states that if ƒ is continuous
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
, then the differential equation has at least one solution in a neighbourhood of the initial condition.
However, it is also possible to consider differential equations with a discontinuous right-hand side, like the equation
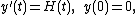
where H denotes the Heaviside function defined by
It makes sense to consider the ramp function
Ramp function
The ramp function is an elementary unary real function, easily computable as the mean of its independent variable and its absolute value.This function is applied in engineering...
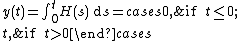
as a solution of the differential equation. Strictly speaking though, it does not satisfy the differential equation at
, because the function is not differentiable there. This suggests that the idea of a solution be extended to allow for solutions that are not everywhere differentiable, thus motivating the following definition.A function y is called a solution in the extended sense of the differential equation
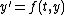with initial condition 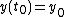if y is absolutely continuousAbsolute continuity
In mathematics, the relationship between the two central operations of calculus, differentiation and integration, stated by fundamental theorem of calculus in the framework of Riemann integration, is generalized in several directions, using Lebesgue integration and absolute continuity...
, y satisfies the differential equation almost everywhere
Almost everywhere
In measure theory , a property holds almost everywhere if the set of elements for which the property does not hold is a null set, that is, a set of measure zero . In cases where the measure is not complete, it is sufficient that the set is contained within a set of measure zero...
and y satisfies the initial condition. The absolute continuity of y implies that its derivative exists almost everywhere.
Statement of the theorem
Consider the differential equation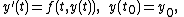with ƒ on the rectangular domain R. If ƒ satisfies the three conditions
- the function ƒ( ·, y) is measurableMeasurable functionIn mathematics, particularly in measure theory, measurable functions are structure-preserving functions between measurable spaces; as such, they form a natural context for the theory of integration...
for every y with |y − y0| ≤ b - the function ƒ(t, ·) is continuous for every t with |t − t0| ≤ a,
- there is a Lebesgue-integrable function m on [t0 − a, t0 + a] such that |ƒ(t, x)| ≤ m(t) for all (t, x) ∈ R,
then the differential equation has a solution in the extended sense in a neighbourhood of the initial condition.