
Cahen's constant
Encyclopedia
In mathematics
, Cahen's constant is defined as an infinite series
of unit fraction
s, with alternating signs, derived from Sylvester's sequence
:
By considering these fractions in pairs, we can also view Cahen's constant as a series of positive unit fractions formed from the terms in even positions of Sylvester's sequence; this series for Cahen's constant forms its greedy Egyptian expansion
: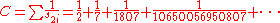
This constant is named after Eugène Cahen (also known for the Cahen-Mellin integral), who first formulated and investigated its series .
Cahen's constant is known to be transcendental
. It is notable as being one of a small number of naturally occurring transcendental numbers for which we know the complete continued fraction
expansion: if we form the sequence
defined by the recurrence
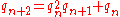
then the continued fraction expansion of Cahen's constant is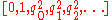
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Cahen's constant is defined as an infinite series
Series (mathematics)
A series is the sum of the terms of a sequence. Finite sequences and series have defined first and last terms, whereas infinite sequences and series continue indefinitely....
of unit fraction
Unit fraction
A unit fraction is a rational number written as a fraction where the numerator is one and the denominator is a positive integer. A unit fraction is therefore the reciprocal of a positive integer, 1/n...
s, with alternating signs, derived from Sylvester's sequence
Sylvester's sequence
In number theory, Sylvester's sequence is an integer sequence in which each member of the sequence is the product of the previous members, plus one. The first few terms of the sequence are:...
:

By considering these fractions in pairs, we can also view Cahen's constant as a series of positive unit fractions formed from the terms in even positions of Sylvester's sequence; this series for Cahen's constant forms its greedy Egyptian expansion
Greedy algorithm for Egyptian fractions
In mathematics, the greedy algorithm for Egyptian fractions is a greedy algorithm, first described by Fibonacci, for transforming rational numbers into Egyptian fractions. An Egyptian fraction is a representation of an irreducible fraction as a sum of unit fractions, as e.g. 5/6 = 1/2 + 1/3...
:
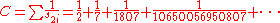
This constant is named after Eugène Cahen (also known for the Cahen-Mellin integral), who first formulated and investigated its series .
Cahen's constant is known to be transcendental
Transcendental number
In mathematics, a transcendental number is a number that is not algebraic—that is, it is not a root of a non-constant polynomial equation with rational coefficients. The most prominent examples of transcendental numbers are π and e...
. It is notable as being one of a small number of naturally occurring transcendental numbers for which we know the complete continued fraction
Continued fraction
In mathematics, a continued fraction is an expression obtained through an iterative process of representing a number as the sum of its integer part and the reciprocal of another number, then writing this other number as the sum of its integer part and another reciprocal, and so on...
expansion: if we form the sequence
- 1, 1, 2, 3, 14, 129, 25298, 420984147, ...
defined by the recurrence
Recurrence
Recurrence and recurrent may refer to:*Recurrence relation, an equation which defines a sequence recursively*Poincaré recurrence theorem, Henri Poincaré's theorem on dynamical systems...
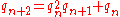
then the continued fraction expansion of Cahen's constant is
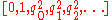
.

