Bron–Kerbosch algorithm
Encyclopedia
In computer science
, the Bron–Kerbosch algorithm is an algorithm
for finding maximal cliques
in an undirected graph
. That is, it lists all subsets of vertices with the two properties that each pair of vertices in one of the listed subsets is connected by an edge, and no listed subset can have any additional vertices added to it while preserving its complete connectivity
. The Bron–Kerbosch algorithm was designed by Dutch scientists Joep Kerbosch and Coenraad Bron
, who published a description of it in 1973. Although other algorithms for solving the clique problem
have running times that are, in theory, better on inputs that have few maximal independent sets, the Bron–Kerbosch algorithm and subsequent improvements to it are frequently reported as being more efficient in practice than the alternatives. It is well-known and widely used in application areas of graph algorithms such as computational chemistry
.
A contemporaneous algorithm of , although presented in different terms, can be viewed as being the same as the Bron–Kerbosch algorithm, as it generates the same recursive search tree.
backtracking
algorithm that searches for all maximal cliques in a given graph G. More generally, given three sets R, P, and X, it finds the maximal cliques that include all of the vertices in R, some of the vertices in P, and none of the vertices in X. Within the recursive calls to the algorithm, P and X are restricted to vertices that form cliques when added to R, as these are the only vertices that can be used as part of the output or to prevent some clique from being reported as output.
The recursion is initiated by setting R and X to be the empty set
and P to be the vertex set of the graph. Within each recursive call, the algorithm considers the vertices in P in turn; if there are no such vertices, it either reports R as a maximal clique (if X is empty), or backtracks. For each vertex v chosen from P, it makes a recursive call in which v is added to R and in which P and X are restricted to neighbors of v, N(v), which finds and reports all clique extensions of R that contain v. Then, it moves v from P to X and continues with the next vertex in P.
That is, in pseudocode, the algorithm performs the following steps:
If the pivot is chosen to minimize the number of recursive calls made by the algorithm, the savings in running time compared to the non-pivoting version of the algorithm can be significant.
The degeneracy
of a graph is the smallest number such that every subgraph of has a vertex with degree
or less. Every graph has a degeneracy ordering, an ordering of the vertices such that each vertex has or fewer neighbors that come later in the ordering; a degeneracy ordering may be found in linear time by repeatedly selecting the vertex of minimum degree among the remaining vertices. If the order of the vertices that the Bron–Kerbosch algorithm loops through is a degeneracy ordering, then the set of candidate vertices in each call (the neighbors of that are later in the ordering) will be guaranteed to have size at most . The set of excluded vertices will consist of all earlier neighbors of , and may be much larger than . In recursive calls to the algorithm below the topmost level of the recursion, the pivoting version can still be used.
In pseudocode, the algorithm performs the following steps:
This variant of the algorithm can be proven to be efficient for graphs of small degeneracy, and experiments show that it also works well in practice for large sparse social network
s and other real-world graphs.
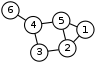In the example graph shown, the algorithm is initially called with R = Ø, P = {1,2,3,4,5,6}, and X = Ø. The pivot u should be chosen as one of the degree-three vertices, to minimize the number of recursive calls; for instance, suppose that u is chosen to be vertex 2. Then there are three remaining vertices in P \ N(u): vertices 2, 4, and 6.
The iteration of the inner loop of the algorithm for v = 2 makes a recursive call to the algorithm with R = {2}, P = {1,3,5}, and X = Ø. Within this recursive call, one of 1 or 5 will be chosen as a pivot, and there will be two second-level recursive calls, one for vertex 3 and the other for whichever vertex was not chosen as pivot. These two calls will eventually report the two cliques {1,2,5} and {2,3}. After returning from these recursive calls, vertex 2 is added to X and removed from P.
The iteration of the inner loop of the algorithm for v = 4 makes a recursive call to the algorithm with R = {4}, P = {3,5,6}, and X = Ø (although vertex 2 belongs to the set X in the outer call to the algorithm, it is not a neighbor of v and is excluded from the subset of X passed to the recursive call). This recursive call will end up making three second-level recursive calls to the algorithm that report the three cliques {3,4}, {4,5}, and {4,6}. Then, vertex 4 is added to X and removed from P.
In the third and final iteration of the inner loop of the algorithm, for v = 6, there is a recursive call to the algorithm with R = {6}, P = Ø, and X = {4}. Because this recursive call has P empty and X non-empty, it immediately backtracks without reporting any more cliques, as there can be no maximal clique that includes vertex 6 and excludes vertex 4.
The call tree for the algorithm, therefore, looks like:
BronKerbosch2(Ø, {1,2,3,4,5,6}, Ø)
BronKerbosch2({2}, {1,3,5}, Ø)
BronKerbosch2({2,3}, Ø, Ø): output {2, 3}
BronKerbosch2({2,5}, {1}, Ø)
BronKerbosch2({1,2,5}, Ø, Ø): output {1,2,5}
BronKerbosch2({4}, {3,5,6}, Ø)
BronKerbosch2({3,4}, Ø, Ø): output {3,4}
BronKerbosch2({4,5}, Ø, Ø): output {4,5}
BronKerbosch2({4,6}, Ø, Ø): output {4,6}
BronKerbosch2({6}, Ø, {4}): no output
The graph in the example has degeneracy two; one possible degeneracy ordering is 6,4,3,1,2,5. If the vertex-ordering version of the Bron–Kerbosch algorithm is applied to the vertices, in this order, the call tree looks like
BronKerbosch3(G)
BronKerbosch2({6}, {4}, Ø)
BronKerbosch2({6,4}, Ø, Ø): output {6,4}
BronKerbosch2({4}, {3,5}, {6})
BronKerbosch2({4,3}, Ø, Ø): output {4,3}
BronKerbosch2({4,5}, Ø, Ø): output {4,5}
BronKerbosch2({3}, {2}, {4})
BronKerbosch2({3,2}, Ø, Ø): output {3,2}
BronKerbosch2({1}, {2,5}, Ø)
BronKerbosch2({1,2}, {5}, Ø)
BronKerbosch2({1,2,5}, Ø, Ø): output {1,2,5}
BronKerbosch2({2}, {5}, {1,3}): no output
BronKerbosch2({5}, Ø, {1,2,4}): no output
: unlike some other algorithms for the clique problem, it does not run in polynomial time per maximal clique generated. However, it is efficient in a worst-case sense: by a result of , any n-vertex graph has at most 3n/3 maximal cliques, and the worst-case running time of the Bron–Kerbosch algorithm (with a pivot strategy that minimizes the number of recursive calls made at each step) is O(3n/3), matching this bound.
For sparse graphs, tighter bounds are possible. In particular the vertex-ordering version of the Bron–Kerbosch algorithm can be made to run in time , where is the degeneracy
of the graph, a measure of its sparseness. There exist -degenerate graphs for which the total number of maximal cliques is , so this bound is close to tight.
Computer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
, the Bron–Kerbosch algorithm is an algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
for finding maximal cliques
Clique (graph theory)
In the mathematical area of graph theory, a clique in an undirected graph is a subset of its vertices such that every two vertices in the subset are connected by an edge. Cliques are one of the basic concepts of graph theory and are used in many other mathematical problems and constructions on graphs...
in an undirected graph
Graph (mathematics)
In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...
. That is, it lists all subsets of vertices with the two properties that each pair of vertices in one of the listed subsets is connected by an edge, and no listed subset can have any additional vertices added to it while preserving its complete connectivity
Complete graph
In the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge.-Properties:...
. The Bron–Kerbosch algorithm was designed by Dutch scientists Joep Kerbosch and Coenraad Bron
Coenraad Bron
Coenraad Bron was a Dutch computer scientist who worked with Edsger W. Dijkstra on Algol-68. Together with Joep Kerbosch he invented the Bron–Kerbosch algorithm for the clique problem....
, who published a description of it in 1973. Although other algorithms for solving the clique problem
Clique problem
In computer science, the clique problem refers to any of the problems related to finding particular complete subgraphs in a graph, i.e., sets of elements where each pair of elements is connected....
have running times that are, in theory, better on inputs that have few maximal independent sets, the Bron–Kerbosch algorithm and subsequent improvements to it are frequently reported as being more efficient in practice than the alternatives. It is well-known and widely used in application areas of graph algorithms such as computational chemistry
Computational chemistry
Computational chemistry is a branch of chemistry that uses principles of computer science to assist in solving chemical problems. It uses the results of theoretical chemistry, incorporated into efficient computer programs, to calculate the structures and properties of molecules and solids...
.
A contemporaneous algorithm of , although presented in different terms, can be viewed as being the same as the Bron–Kerbosch algorithm, as it generates the same recursive search tree.
Without pivoting
The basic form of the Bron–Kerbosch algorithm is a recursiveRecursion
Recursion is the process of repeating items in a self-similar way. For instance, when the surfaces of two mirrors are exactly parallel with each other the nested images that occur are a form of infinite recursion. The term has a variety of meanings specific to a variety of disciplines ranging from...
backtracking
Backtracking
Backtracking is a general algorithm for finding all solutions to some computational problem, that incrementally builds candidates to the solutions, and abandons each partial candidate c as soon as it determines that c cannot possibly be completed to a valid solution.The classic textbook example...
algorithm that searches for all maximal cliques in a given graph G. More generally, given three sets R, P, and X, it finds the maximal cliques that include all of the vertices in R, some of the vertices in P, and none of the vertices in X. Within the recursive calls to the algorithm, P and X are restricted to vertices that form cliques when added to R, as these are the only vertices that can be used as part of the output or to prevent some clique from being reported as output.
The recursion is initiated by setting R and X to be the empty set
Empty set
In mathematics, and more specifically set theory, the empty set is the unique set having no elements; its size or cardinality is zero. Some axiomatic set theories assure that the empty set exists by including an axiom of empty set; in other theories, its existence can be deduced...
and P to be the vertex set of the graph. Within each recursive call, the algorithm considers the vertices in P in turn; if there are no such vertices, it either reports R as a maximal clique (if X is empty), or backtracks. For each vertex v chosen from P, it makes a recursive call in which v is added to R and in which P and X are restricted to neighbors of v, N(v), which finds and reports all clique extensions of R that contain v. Then, it moves v from P to X and continues with the next vertex in P.
That is, in pseudocode, the algorithm performs the following steps:
BronKerbosch1(R,P,X):
if P and X are both empty:
report R as a maximal clique
for each vertex v in P:
BronKerbosch1(R ⋃ {v}, P ⋂ N(v), X ⋂ N(v))
P := P \ {v}
X := X ⋃ {v}
With pivoting
The basic form of the algorithm, described above, is inefficient in the case of graphs with many non-maximal cliques: it makes a recursive call for every clique, maximal or not. To save time and allow the algorithm to backtrack more quickly in branches of the search that contain no maximal cliques, Bron and Kerbosch introduced a variant of the algorithm involving a "pivot vertex" u, chosen from P (or more generally, as later investigators realized, from P ⋃ X). Any maximal clique must include either u or one of its non-neighbors, for otherwise the clique could be augmented by adding u to it. Therefore, only u and its non-neighbors need to be tested as the choices for the vertex v that is added to R in each recursive call to the algorithm. In pseudocode:
BronKerbosch2(R,P,X):
if P and X are both empty:
report R as a maximal clique
choose a pivot vertex u in P ⋃ X
for each vertex v in P \ N(u):
BronKerbosch2(R ⋃ {v}, P ⋂ N(v), X ⋂ N(v))
P := P \ {v}
X := X ⋃ {v}
If the pivot is chosen to minimize the number of recursive calls made by the algorithm, the savings in running time compared to the non-pivoting version of the algorithm can be significant.
With vertex ordering
An alternative method for improving the basic form of the Bron–Kerbosch algorithm involves forgoing pivoting at the outermost level of recursion, and instead choosing the ordering of the recursive calls carefully in order to minimize the sizes of the sets of candidate vertices within each recursive call.The degeneracy
Degeneracy (graph theory)
In graph theory, a k-degenerate graph is an undirected graph in which every subgraph has a vertex of degree at most k: that is, some vertex in the subgraph touches k or fewer of the subgraph's edges. The degeneracy of a graph is the smallest value of k for which it is k-degenerate...
of a graph is the smallest number such that every subgraph of has a vertex with degree
Degree (graph theory)
In graph theory, the degree of a vertex of a graph is the number of edges incident to the vertex, with loops counted twice. The degree of a vertex v is denoted \deg. The maximum degree of a graph G, denoted by Δ, and the minimum degree of a graph, denoted by δ, are the maximum and minimum degree...
or less. Every graph has a degeneracy ordering, an ordering of the vertices such that each vertex has or fewer neighbors that come later in the ordering; a degeneracy ordering may be found in linear time by repeatedly selecting the vertex of minimum degree among the remaining vertices. If the order of the vertices that the Bron–Kerbosch algorithm loops through is a degeneracy ordering, then the set of candidate vertices in each call (the neighbors of that are later in the ordering) will be guaranteed to have size at most . The set of excluded vertices will consist of all earlier neighbors of , and may be much larger than . In recursive calls to the algorithm below the topmost level of the recursion, the pivoting version can still be used.
In pseudocode, the algorithm performs the following steps:
BronKerbosch3(G):
P = V(G)
R = X = empty
for each vertex v in a degeneracy ordering of G:
BronKerbosch2(R ⋃ {v}, P ⋂ N(v), X ⋂ N(v))
P := P \ {v}
X := X ⋃ {v}
This variant of the algorithm can be proven to be efficient for graphs of small degeneracy, and experiments show that it also works well in practice for large sparse social network
Social network
A social network is a social structure made up of individuals called "nodes", which are tied by one or more specific types of interdependency, such as friendship, kinship, common interest, financial exchange, dislike, sexual relationships, or relationships of beliefs, knowledge or prestige.Social...
s and other real-world graphs.
Example
The iteration of the inner loop of the algorithm for v = 2 makes a recursive call to the algorithm with R = {2}, P = {1,3,5}, and X = Ø. Within this recursive call, one of 1 or 5 will be chosen as a pivot, and there will be two second-level recursive calls, one for vertex 3 and the other for whichever vertex was not chosen as pivot. These two calls will eventually report the two cliques {1,2,5} and {2,3}. After returning from these recursive calls, vertex 2 is added to X and removed from P.
The iteration of the inner loop of the algorithm for v = 4 makes a recursive call to the algorithm with R = {4}, P = {3,5,6}, and X = Ø (although vertex 2 belongs to the set X in the outer call to the algorithm, it is not a neighbor of v and is excluded from the subset of X passed to the recursive call). This recursive call will end up making three second-level recursive calls to the algorithm that report the three cliques {3,4}, {4,5}, and {4,6}. Then, vertex 4 is added to X and removed from P.
In the third and final iteration of the inner loop of the algorithm, for v = 6, there is a recursive call to the algorithm with R = {6}, P = Ø, and X = {4}. Because this recursive call has P empty and X non-empty, it immediately backtracks without reporting any more cliques, as there can be no maximal clique that includes vertex 6 and excludes vertex 4.
The call tree for the algorithm, therefore, looks like:
BronKerbosch2(Ø, {1,2,3,4,5,6}, Ø)
BronKerbosch2({2}, {1,3,5}, Ø)
BronKerbosch2({2,3}, Ø, Ø): output {2, 3}
BronKerbosch2({2,5}, {1}, Ø)
BronKerbosch2({1,2,5}, Ø, Ø): output {1,2,5}
BronKerbosch2({4}, {3,5,6}, Ø)
BronKerbosch2({3,4}, Ø, Ø): output {3,4}
BronKerbosch2({4,5}, Ø, Ø): output {4,5}
BronKerbosch2({4,6}, Ø, Ø): output {4,6}
BronKerbosch2({6}, Ø, {4}): no output
The graph in the example has degeneracy two; one possible degeneracy ordering is 6,4,3,1,2,5. If the vertex-ordering version of the Bron–Kerbosch algorithm is applied to the vertices, in this order, the call tree looks like
BronKerbosch3(G)
BronKerbosch2({6}, {4}, Ø)
BronKerbosch2({6,4}, Ø, Ø): output {6,4}
BronKerbosch2({4}, {3,5}, {6})
BronKerbosch2({4,3}, Ø, Ø): output {4,3}
BronKerbosch2({4,5}, Ø, Ø): output {4,5}
BronKerbosch2({3}, {2}, {4})
BronKerbosch2({3,2}, Ø, Ø): output {3,2}
BronKerbosch2({1}, {2,5}, Ø)
BronKerbosch2({1,2}, {5}, Ø)
BronKerbosch2({1,2,5}, Ø, Ø): output {1,2,5}
BronKerbosch2({2}, {5}, {1,3}): no output
BronKerbosch2({5}, Ø, {1,2,4}): no output
Worst-case analysis
The Bron–Kerbosch algorithm is not an output-sensitive algorithmOutput-sensitive algorithm
In computer science, an output-sensitive algorithm is an algorithm whose running time depends not only on the size of the input but also on the size of the output...
: unlike some other algorithms for the clique problem, it does not run in polynomial time per maximal clique generated. However, it is efficient in a worst-case sense: by a result of , any n-vertex graph has at most 3n/3 maximal cliques, and the worst-case running time of the Bron–Kerbosch algorithm (with a pivot strategy that minimizes the number of recursive calls made at each step) is O(3n/3), matching this bound.
For sparse graphs, tighter bounds are possible. In particular the vertex-ordering version of the Bron–Kerbosch algorithm can be made to run in time , where is the degeneracy
Degeneracy (graph theory)
In graph theory, a k-degenerate graph is an undirected graph in which every subgraph has a vertex of degree at most k: that is, some vertex in the subgraph touches k or fewer of the subgraph's edges. The degeneracy of a graph is the smallest value of k for which it is k-degenerate...
of the graph, a measure of its sparseness. There exist -degenerate graphs for which the total number of maximal cliques is , so this bound is close to tight.
External links
- Bron-Kerbosh algorithm implementation in Python
- Finding all cliques of an undirected graph. Seminar notes by Michaela Regneri, January 11, 2007.