
Brocard point
Encyclopedia
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, Brocard points are special points within a triangle
Triangle
A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted ....
. They are named after Henri Brocard
Henri Brocard
Pierre René Jean Baptiste Henri Brocard was a French meteorologist and mathematician, in particular a geometer...
(1845 – 1922), a French mathematician.
Definition
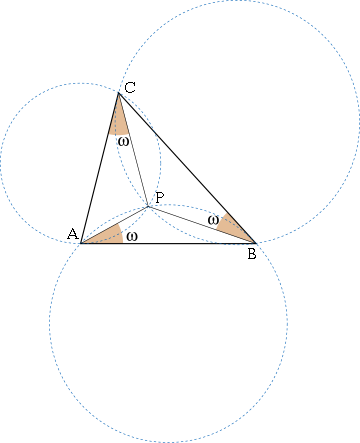
In a triangle ABC with sides a, b, and c, where the vertices are labeled A, B and C in counterclockwise order, there is exactly one point P such that the line segments AP, BP, and CP form the same angle, ω, with the respective sides c, a, and b, namely thatPoint P is called the first Brocard point of the triangle ABC, and the angle ω is called the Brocard angle of the triangle. The following applies to this angle:

There is also a second Brocard point, Q, in triangle ABC such that line segments AQ, BQ, and CQ form equal angles with sides b, c, and a respectively. In other words, the equations
 apply. Remarkably, this second Brocard point has the same Brocard angle as the first Brocard point. In other words angle
apply. Remarkably, this second Brocard point has the same Brocard angle as the first Brocard point. In other words angle  is the same as
is the same as 
The two Brocard points are closely related to one another; In fact, the difference between the first and the second depends on the order in which the angles of triangle ABC are taken. So for example, the first Brocard point of triangle ABC is the same as the second Brocard point of triangle ACB.
The two Brocard points of a triangle ABC are isogonal conjugate
Isogonal conjugate
In geometry, the isogonal conjugate of a point P with respect to a triangle ABC is constructed by reflecting the lines PA, PB, and PC about the angle bisectors of A, B, and C. These three reflected lines concur at the isogonal conjugate of P...
s of each other.
Construction
The most elegant construction of the Brocard points goes as follows. In the following example the first Brocard point is presented, but the construction for the second Brocard point is very similar.Form a circle through points A and B, tangent to edge BC of the triangle (the center of this circle is at the point where the perpendicular bisector of AB meets the line through point B that is perpendicular to BC). Symmetrically, form a circle through points B and C, tangent to edge AC, and a circle through points A and C, tangent to edge AB. These three circles have a common point, the first Brocard point of triangle ABC. See also Tangent lines to circles
Tangent lines to circles
In Euclidean plane geometry, tangent lines to circles form the subject of several theorems, and play an important role in many geometrical constructions and proofs...
.
The three circles just constructed are also designated as epicycles of triangle ABC. The second Brocard point is constructed in similar fashion.
Trilinears and the Brocard midpoint
Homogeneous trilinear coordinatesTrilinear coordinates
In geometry, the trilinear coordinates of a point relative to a given triangle describe the relative distances from the three sides of the triangle. Trilinear coordinates are an example of homogeneous coordinates...
for the first and second Brocard points are c/b : a/c : b/a, and b/c : c/a : a/b, respectively. They are an example of a bicentric pair of points, but not triangle centers. Their midpoint, called the Brocard midpoint, has trilinears
- sin(A + ω) : sin(B + ω) : sin(C + ω)
and is a triangle center. The third Brocard point, given in trilinear coordinates
Trilinear coordinates
In geometry, the trilinear coordinates of a point relative to a given triangle describe the relative distances from the three sides of the triangle. Trilinear coordinates are an example of homogeneous coordinates...
as a−3 : b−3 : c−3, or, equivalently, by
- csc(A − ω) : csc(B − ω) : csc(C − ω),
is the Brocard midpoint of the anticomplementary triangle and is also the isotomic conjugate
Isotomic conjugate
In geometry, the isotomic conjugate of a point P not on a sideline of triangle ABC is constructed as follows: Let A, B, C be the points in which the lines AP, BP, CP meet the lines BC, CA, AB, respectively. Reflect ABC in the midpoints of sides BC, CA, AB to obtain points A", B", C", respectively...
of the symmedian point.
External links
- Third Brocard Point at MathWorld
- Bicentric Pairs of Points and Related Triangle Centers
- Bicentric Pairs of Points
- Bicentric Points at MathWorld


