Brauer's theorem on induced characters
Encyclopedia
Brauer's theorem on induced characters, often known as Brauer's induction theorem, and named after Richard Brauer
, is a basic result in the branch of mathematics
known as character theory
, which is, in turn, part of the representation theory of a finite group. Let G be a finite group
and let Char(G) denote the subring of the ring of complex-valued class function
s of G consisting of integer combinations of irreducible characters
. Char(G) is known as the character ring of G, and its elements are known as virtual characters (alternatively, as generalized characters, or sometimes difference characters). It is a ring by virtue of the fact that the product of characters of G is again a character of G. Its multiplication is given by the elementwise product of class functions.
Brauer's induction theorem shows that the character ring can be generated (as an abelian group
) by certain characters which are fairly easily understood. More precisely, the theorem states that every virtual character of G is expressible as an integer combination of induced character
s of the form ,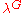
, where H ranges over subgroup
s of G and λ ranges over linear character
s (having degree 1) of H.
In fact, Brauer showed that the subgroups H could be chosen from a very
restricted collection, now called Brauer elementary
subgroups
. These are direct products of cyclic groups and groups whose order is a power of a prime.
Using Frobenius reciprocity
, Brauer's induction theorem leads easily to his fundamental characterization of characters, which asserts that a complex-valued class function of G is a virtual character if and only if its restriction to each Brauer elementary subgroup of G is a virtual character. This result, together with the fact that a virtual character θ is an irreducible character
if and only if θ(1) > 0 and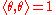
(where 
is the usual inner product on the ring of complex-valued class functions) gives
a means of constructing irreducible characters without explicitly constructing the associated representations.
An initial motivation for Brauer's induction theorem was application to Artin L-function
s. It shows that those are built up from Dirichlet L-functions, or more general Hecke L-functions. Highly significant for that application is whether each character of G is a non-negative integer combination of characters induced from linear characters of subgroups. In general, this is not the case. In fact, by a theorem of Taketa, if all characters of G are so expressible, then G must be a solvable group
(although solvability alone does not guarantee such expressions- for example, the solvable group SL(2,3) has an irreducible complex character of degree 2 which is not expressible as a non-negative integer combination of characters induced from linear characters of subgroups). An ingredient of the proof of Brauer's induction theorem is that when G is a finite nilpotent group
, every complex irreducible character of G is induced from a linear character of some subgroup.
A precursor to Brauer's induction theorem was Artin's induction theorem
, which states that |G| times the trivial character of G is an integer combination of characters which are each induced from trivial characters of cyclic subgroups of G. Brauer's theorem removes the factor |G|,
but at the expense of expanding the collection of subgroups used. Some years after the proof of Brauer's theorem appeared, J.A. Green
showed (in 1955) that no such induction theorem (with integer combinations of characters induced from linear characters) could be proved with a collection of subgroups smaller than the Brauer elementary subgroups.
The proof of Brauer's induction theorem exploits the ring structure of Char(G) (most proofs also make use of a slightly larger ring, Char*(G), which consists of
-combinations of irreducible characters, where ω is a primitive complex |G|-th root of unity). The set of integer combinations of characters induced from linear characters of Brauer elementary subgroups is an ideal I(G) of Char(G), so the proof reduces to showing that the trivial character is in I(G). Several proofs of the theorem, beginning with a proof due to Brauer and John Tate
, show that the trivial character is in the analogously defined ideal I*(G) of Char*(G) by concentrating attention on one prime p at a time, and constructing integer-valued elements of I*(G) which differ (elementwise) from the trivial character by (integer multiples of) a sufficiently high power of p. Once this is achieved for every prime divisor of |G|, some manipulations with congruences
and algebraic integer
s, again exploiting the fact that I*(G) is an ideal of Ch*(G), place the trivial character in I(G). An auxiliary result here is that a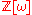
-valued class function lies in the ideal I*(G) if its values are all divisible (in 
) by |G|.
Brauer's induction theorem was proved in 1946, and there are now many alternative proofs. In 1986, Victor Snaith gave a proof by a radically different approach, topological in nature (an application of the Lefschetz fixed-point theorem
). There has been related recent work on the question of finding natural and explicit forms of Brauer's theorem, notably by Robert Boltje.
Richard Brauer
Richard Dagobert Brauer was a leading German and American mathematician. He worked mainly in abstract algebra, but made important contributions to number theory...
, is a basic result in the branch of mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
known as character theory
Character theory
In mathematics, more specifically in group theory, the character of a group representation is a function on the group which associates to each group element the trace of the corresponding matrix....
, which is, in turn, part of the representation theory of a finite group. Let G be a finite group
Finite group
In mathematics and abstract algebra, a finite group is a group whose underlying set G has finitely many elements. During the twentieth century, mathematicians investigated certain aspects of the theory of finite groups in great depth, especially the local theory of finite groups, and the theory of...
and let Char(G) denote the subring of the ring of complex-valued class function
Class function
In mathematics, especially in the fields of group theory and representation theory of groups, a class function is a function f on a group G, such that f is constant on the conjugacy classes of G. In other words, f is invariant under the conjugation map on G...
s of G consisting of integer combinations of irreducible characters
Character theory
In mathematics, more specifically in group theory, the character of a group representation is a function on the group which associates to each group element the trace of the corresponding matrix....
. Char(G) is known as the character ring of G, and its elements are known as virtual characters (alternatively, as generalized characters, or sometimes difference characters). It is a ring by virtue of the fact that the product of characters of G is again a character of G. Its multiplication is given by the elementwise product of class functions.
Brauer's induction theorem shows that the character ring can be generated (as an abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
) by certain characters which are fairly easily understood. More precisely, the theorem states that every virtual character of G is expressible as an integer combination of induced character
Character theory
In mathematics, more specifically in group theory, the character of a group representation is a function on the group which associates to each group element the trace of the corresponding matrix....
s of the form ,
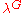, where H ranges over subgroupSubgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
s of G and λ ranges over linear character
Character theory
In mathematics, more specifically in group theory, the character of a group representation is a function on the group which associates to each group element the trace of the corresponding matrix....
s (having degree 1) of H.
In fact, Brauer showed that the subgroups H could be chosen from a very
restricted collection, now called Brauer elementary
subgroups
Elementary group
In algebra, more specifically group theory, a p-elementary group is a direct product of a finite cyclic group of order relatively prime to p and a p-group. A finite group is an elementary group if it is p-elementary for some prime number p...
. These are direct products of cyclic groups and groups whose order is a power of a prime.
Using Frobenius reciprocity
Character theory
In mathematics, more specifically in group theory, the character of a group representation is a function on the group which associates to each group element the trace of the corresponding matrix....
, Brauer's induction theorem leads easily to his fundamental characterization of characters, which asserts that a complex-valued class function of G is a virtual character if and only if its restriction to each Brauer elementary subgroup of G is a virtual character. This result, together with the fact that a virtual character θ is an irreducible character
if and only if θ(1) > 0 and
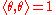(where is the usual inner product on the ring of complex-valued class functions) givesa means of constructing irreducible characters without explicitly constructing the associated representations.
An initial motivation for Brauer's induction theorem was application to Artin L-function
Artin L-function
In mathematics, an Artin L-function is a type of Dirichlet series associated to a linear representation ρ of a Galois group G. These functions were introduced in the 1923 by Emil Artin, in connection with his research into class field theory. Their fundamental properties, in particular the Artin...
s. It shows that those are built up from Dirichlet L-functions, or more general Hecke L-functions. Highly significant for that application is whether each character of G is a non-negative integer combination of characters induced from linear characters of subgroups. In general, this is not the case. In fact, by a theorem of Taketa, if all characters of G are so expressible, then G must be a solvable group
Group theory
In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
(although solvability alone does not guarantee such expressions- for example, the solvable group SL(2,3) has an irreducible complex character of degree 2 which is not expressible as a non-negative integer combination of characters induced from linear characters of subgroups). An ingredient of the proof of Brauer's induction theorem is that when G is a finite nilpotent group
Group theory
In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
, every complex irreducible character of G is induced from a linear character of some subgroup.
A precursor to Brauer's induction theorem was Artin's induction theorem
Emil Artin
Emil Artin was an Austrian-American mathematician of Armenian descent.-Parents:Emil Artin was born in Vienna to parents Emma Maria, née Laura , a soubrette on the operetta stages of Austria and Germany, and Emil Hadochadus Maria Artin, Austrian-born of Armenian descent...
, which states that |G| times the trivial character of G is an integer combination of characters which are each induced from trivial characters of cyclic subgroups of G. Brauer's theorem removes the factor |G|,
but at the expense of expanding the collection of subgroups used. Some years after the proof of Brauer's theorem appeared, J.A. Green
James Alexander Green
James Alexander "Sandy" Green FRS is a mathematician and retired Professor at the Mathematics Institute at the University of Warwick, who is still active in the field of representation theory.-Early life:...
showed (in 1955) that no such induction theorem (with integer combinations of characters induced from linear characters) could be proved with a collection of subgroups smaller than the Brauer elementary subgroups.
The proof of Brauer's induction theorem exploits the ring structure of Char(G) (most proofs also make use of a slightly larger ring, Char*(G), which consists of
-combinations of irreducible characters, where ω is a primitive complex |G|-th root of unity). The set of integer combinations of characters induced from linear characters of Brauer elementary subgroups is an ideal I(G) of Char(G), so the proof reduces to showing that the trivial character is in I(G). Several proofs of the theorem, beginning with a proof due to Brauer and John TateJohn Tate
John Torrence Tate Jr. is an American mathematician, distinguished for many fundamental contributions in algebraic number theory, arithmetic geometry and related areas in algebraic geometry.-Biography:...
, show that the trivial character is in the analogously defined ideal I*(G) of Char*(G) by concentrating attention on one prime p at a time, and constructing integer-valued elements of I*(G) which differ (elementwise) from the trivial character by (integer multiples of) a sufficiently high power of p. Once this is achieved for every prime divisor of |G|, some manipulations with congruences
and algebraic integer
Algebraic integer
In number theory, an algebraic integer is a complex number that is a root of some monic polynomial with coefficients in . The set of all algebraic integers is closed under addition and multiplication and therefore is a subring of complex numbers denoted by A...
s, again exploiting the fact that I*(G) is an ideal of Ch*(G), place the trivial character in I(G). An auxiliary result here is that a
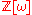-valued class function lies in the ideal I*(G) if its values are all divisible (in ) by |G|.Brauer's induction theorem was proved in 1946, and there are now many alternative proofs. In 1986, Victor Snaith gave a proof by a radically different approach, topological in nature (an application of the Lefschetz fixed-point theorem
Lefschetz fixed-point theorem
In mathematics, the Lefschetz fixed-point theorem is a formula that counts the fixed points of a continuous mapping from a compact topological space X to itself by means of traces of the induced mappings on the homology groups of X...
). There has been related recent work on the question of finding natural and explicit forms of Brauer's theorem, notably by Robert Boltje.