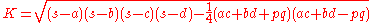
Brahmagupta's formula
Encyclopedia
In Euclidean geometry
, Brahmagupta
's formula finds the area
of any quadrilateral
given the lengths of the sides and some of the angles. In its most common form, it yields the area of quadrilaterals that can be inscribed in a circle
.
whose sides have lengths a, b, c, d as
where s, the semiperimeter
, is

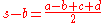
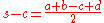
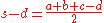
This formula generalizes Heron's formula for the area of a triangle
. In fact, Heron's formula may be derived from Brahmagupta's formula by allowing d to approach a value of zero. A triangle may be regarded as a quadrilateral with one side of length zero. From this perspective, as d approaches zero, a cyclic quadrilateral converges into a cyclic triangle (all triangles are cyclic), and Brahmagupta's formula converges into Heron's formula.
The assertion that the area of the quadrilateral is given by Brahmagupta's formula is equivalent to the assertion that it is equal to
Brahmagupta's formula may be seen as a formula in the half-lengths of the sides, but it also gives the area as a formula in the altitudes from the center to the sides, although if the quadrilateral does not contain the center, the altitude to the longest side must be taken as negative.
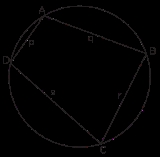
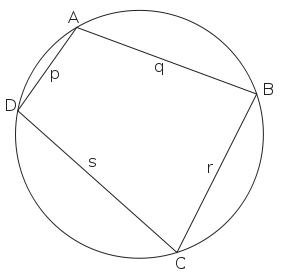 Here we use the notations in the figure to the right. Area of the cyclic quadrilateral = Area of
Here we use the notations in the figure to the right. Area of the cyclic quadrilateral = Area of  + Area of
+ Area of 
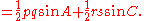
But since is a cyclic quadrilateral,
is a cyclic quadrilateral, 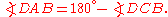 Hence
Hence  Therefore
Therefore


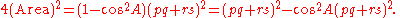
Solving for common side DB, in ADB and
ADB and  BDC, the law of cosines
BDC, the law of cosines
gives
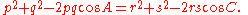
Substituting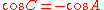 (since angles
(since angles  and
and  are supplementary
are supplementary
) and rearranging, we have
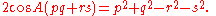
Substituting this in the equation for the area,
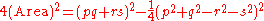
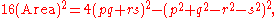
which is of the form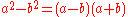 and hence can be written as
and hence can be written as
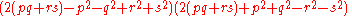
which, regrouping, is of the form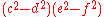

hence yielding four linear factors: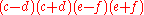

Introducing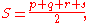
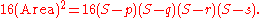
Taking the square root, we get

of the quadrilateral:
where θ is half the sum of two opposite angles. (The pair is irrelevant: if the other two angles are taken, half their sum is the supplement of θ. Since cos(180° − θ) = −cosθ, we have cos2(180° − θ) = cos2θ.) It follows from this fact that the area of a cyclic quadrilateral is the maximum possible area for any quadrilateral with the given side lengths. This more general formula is sometimes known as Bretschneider's formula.
It is a property of cyclic quadrilateral
s (and ultimately of inscribed angle
s) that opposite angles of a quadrilateral sum to 180°. Consequently, in the case of an inscribed quadrilateral, θ = 90°, whence the term
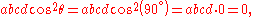
giving the basic form of Brahmagupta's formula.
A related formula, which was proved by Coolidge
, also gives the area of a general convex quadrilateral. It is
where p and q are the lengths of the diagonals of the quadrilateral. In a cyclic quadrilateral
,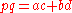 according to Ptolemy's theorem
according to Ptolemy's theorem
, and the formula of Coolidge reduces to Brahmagupta's formula.
Euclidean geometry
Euclidean geometry is a mathematical system attributed to the Alexandrian Greek mathematician Euclid, which he described in his textbook on geometry: the Elements. Euclid's method consists in assuming a small set of intuitively appealing axioms, and deducing many other propositions from these...
, Brahmagupta
Brahmagupta
Brahmagupta was an Indian mathematician and astronomer who wrote many important works on mathematics and astronomy. His best known work is the Brāhmasphuṭasiddhānta , written in 628 in Bhinmal...
's formula finds the area
Area
Area is a quantity that expresses the extent of a two-dimensional surface or shape in the plane. Area can be understood as the amount of material with a given thickness that would be necessary to fashion a model of the shape, or the amount of paint necessary to cover the surface with a single coat...
of any quadrilateral
Quadrilateral
In Euclidean plane geometry, a quadrilateral is a polygon with four sides and four vertices or corners. Sometimes, the term quadrangle is used, by analogy with triangle, and sometimes tetragon for consistency with pentagon , hexagon and so on...
given the lengths of the sides and some of the angles. In its most common form, it yields the area of quadrilaterals that can be inscribed in a circle
Circle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
.
Basic form
In its basic and easiest-to-remember form, Brahmagupta's formula gives the area K of a cyclic quadrilateralCyclic quadrilateral
In Euclidean geometry, a cyclic quadrilateral is a quadrilateral whose vertices all lie on a single circle. This circle is called the circumcircle or circumscribed circle, and the vertices are said to be concyclic. Other names for these quadrilaterals are chordal quadrilateral and inscribed...
whose sides have lengths a, b, c, d as
where s, the semiperimeter
Semiperimeter
In geometry, the semiperimeter of a polygon is half its perimeter. Although it has such a simple derivation from the perimeter, the semiperimeter appears frequently enough in formulas for triangles and other figures that it is given a separate name...
, is

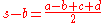
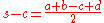
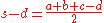
This formula generalizes Heron's formula for the area of a triangle
Triangle
A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted ....
. In fact, Heron's formula may be derived from Brahmagupta's formula by allowing d to approach a value of zero. A triangle may be regarded as a quadrilateral with one side of length zero. From this perspective, as d approaches zero, a cyclic quadrilateral converges into a cyclic triangle (all triangles are cyclic), and Brahmagupta's formula converges into Heron's formula.
The assertion that the area of the quadrilateral is given by Brahmagupta's formula is equivalent to the assertion that it is equal to
Brahmagupta's formula may be seen as a formula in the half-lengths of the sides, but it also gives the area as a formula in the altitudes from the center to the sides, although if the quadrilateral does not contain the center, the altitude to the longest side must be taken as negative.
Proof of Brahmagupta's formula

 + Area of
+ Area of 
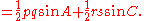
But since
 is a cyclic quadrilateral,
is a cyclic quadrilateral, 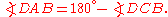 Hence
Hence  Therefore
Therefore

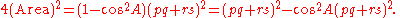
Solving for common side DB, in
 ADB and
ADB and  BDC, the law of cosines
BDC, the law of cosinesLaw of cosines
In trigonometry, the law of cosines relates the lengths of the sides of a plane triangle to the cosine of one of its angles. Using notation as in Fig...
gives
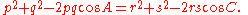
Substituting
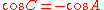 (since angles
(since angles  and
and  are supplementary
are supplementarySupplementary angles
Supplementary angles are pairs of angles that add up to 180 degrees. Thus the supplement of an angle of x degrees is an angle of degrees....
) and rearranging, we have
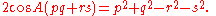
Substituting this in the equation for the area,
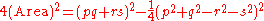
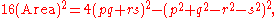
which is of the form
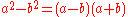 and hence can be written as
and hence can be written as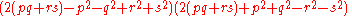
which, regrouping, is of the form
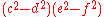

hence yielding four linear factors:
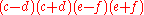

Introducing
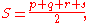
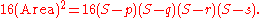
Taking the square root, we get

Extension to non-cyclic quadrilaterals
In the case of non-cyclic quadrilaterals, Brahmagupta's formula can be extended by considering the measures of two opposite anglesAngles
The Angles is a modern English term for a Germanic people who took their name from the ancestral cultural region of Angeln, a district located in Schleswig-Holstein, Germany...
of the quadrilateral:
where θ is half the sum of two opposite angles. (The pair is irrelevant: if the other two angles are taken, half their sum is the supplement of θ. Since cos(180° − θ) = −cosθ, we have cos2(180° − θ) = cos2θ.) It follows from this fact that the area of a cyclic quadrilateral is the maximum possible area for any quadrilateral with the given side lengths. This more general formula is sometimes known as Bretschneider's formula.
It is a property of cyclic quadrilateral
Cyclic quadrilateral
In Euclidean geometry, a cyclic quadrilateral is a quadrilateral whose vertices all lie on a single circle. This circle is called the circumcircle or circumscribed circle, and the vertices are said to be concyclic. Other names for these quadrilaterals are chordal quadrilateral and inscribed...
s (and ultimately of inscribed angle
Inscribed angle
In geometry, an inscribed angle is formed when two secant lines of a circle intersect on the circle....
s) that opposite angles of a quadrilateral sum to 180°. Consequently, in the case of an inscribed quadrilateral, θ = 90°, whence the term
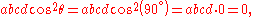
giving the basic form of Brahmagupta's formula.
A related formula, which was proved by Coolidge
Julian Coolidge
Julian Lowell Coolidge was an American mathematician and a professor and chairman of the Harvard University Mathematics Department.-Biography:...
, also gives the area of a general convex quadrilateral. It is
where p and q are the lengths of the diagonals of the quadrilateral. In a cyclic quadrilateral
Cyclic quadrilateral
In Euclidean geometry, a cyclic quadrilateral is a quadrilateral whose vertices all lie on a single circle. This circle is called the circumcircle or circumscribed circle, and the vertices are said to be concyclic. Other names for these quadrilaterals are chordal quadrilateral and inscribed...
,
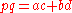 according to Ptolemy's theorem
according to Ptolemy's theoremPtolemy's theorem
In Euclidean geometry, Ptolemy's theorem is a relation between the four sides and two diagonals of a cyclic quadrilateral . The theorem is named after the Greek astronomer and mathematician Ptolemy...
, and the formula of Coolidge reduces to Brahmagupta's formula.
Related theorems
- Heron's formula for the area of a triangleTriangleA triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted ....
is the special case obtained by taking d = 0. - The relationship between the general and extended form of Brahmagupta's formula is similar to how the law of cosinesLaw of cosinesIn trigonometry, the law of cosines relates the lengths of the sides of a plane triangle to the cosine of one of its angles. Using notation as in Fig...
extends the Pythagorean theoremPythagorean theoremIn mathematics, the Pythagorean theorem or Pythagoras' theorem is a relation in Euclidean geometry among the three sides of a right triangle...
.