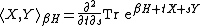Bogoliubov inner product
Encyclopedia
The Bogoliubov inner product (Duhamel two-point function, Bogolyubov inner product, Bogoliubov scalar product, Kubo
-Mori-Bogoliubov inner product) is a special inner product in the space of operators. The Bogoliubov inner product appears in quantum statistical mechanics
and is named after theoretical physicist Nikolay Bogoliubov.
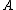 be a self-adjoint operator
be a self-adjoint operator
. The Bogoliubov inner product of any two operators X and Y is defined as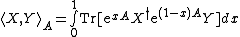
The Bogoliubov inner product satisfies all the axioms of the inner product: it is sesquilinear
, positive semidefinite (i.e.,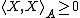 ), and satisfies the symmetry property
), and satisfies the symmetry property 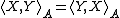 .
.
In applications to quantum statistical mechanics
, the operator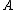 has the form
has the form  , where
, where 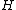 is the Hamiltonian
is the Hamiltonian
of the quantum system and is the inverse temperature. With these notations, the Bogoliubov inner product takes the form
is the inverse temperature. With these notations, the Bogoliubov inner product takes the form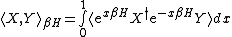
where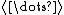 denotes the thermal average with respect to the Hamiltonian
denotes the thermal average with respect to the Hamiltonian 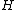 and inverse temperature
and inverse temperature 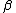 .
.
In quantum statistical mechanics, the Bogoliubov inner product appears as the second order term in the expansion of the statistical sum: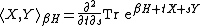
Ryogo Kubo
was a Japanese mathematical physicist, best known for his works in statistical physics and non-equilibrium statistical mechanics.In the early 1950s, Kubo transformed research into the linear response properties of near-equilibrium condensed-matter systems, in particular the understanding of...
-Mori-Bogoliubov inner product) is a special inner product in the space of operators. The Bogoliubov inner product appears in quantum statistical mechanics
Quantum statistical mechanics
Quantum statistical mechanics is the study of statistical ensembles of quantum mechanical systems. A statistical ensemble is described by a density operator S, which is a non-negative, self-adjoint, trace-class operator of trace 1 on the Hilbert space H describing the quantum system. This can be...
and is named after theoretical physicist Nikolay Bogoliubov.
Definition
Let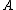 be a self-adjoint operator
be a self-adjoint operatorSelf-adjoint operator
In mathematics, on a finite-dimensional inner product space, a self-adjoint operator is an operator that is its own adjoint, or, equivalently, one whose matrix is Hermitian, where a Hermitian matrix is one which is equal to its own conjugate transpose...
. The Bogoliubov inner product of any two operators X and Y is defined as
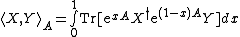
The Bogoliubov inner product satisfies all the axioms of the inner product: it is sesquilinear
Sesquilinear form
In mathematics, a sesquilinear form on a complex vector space V is a map V × V → C that is linear in one argument and antilinear in the other. The name originates from the numerical prefix sesqui- meaning "one and a half"...
, positive semidefinite (i.e.,
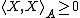 ), and satisfies the symmetry property
), and satisfies the symmetry property 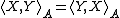 .
.In applications to quantum statistical mechanics
Quantum statistical mechanics
Quantum statistical mechanics is the study of statistical ensembles of quantum mechanical systems. A statistical ensemble is described by a density operator S, which is a non-negative, self-adjoint, trace-class operator of trace 1 on the Hilbert space H describing the quantum system. This can be...
, the operator
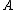 has the form
has the form  , where
, where 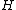 is the Hamiltonian
is the HamiltonianHamiltonian (quantum mechanics)
In quantum mechanics, the Hamiltonian H, also Ȟ or Ĥ, is the operator corresponding to the total energy of the system. Its spectrum is the set of possible outcomes when one measures the total energy of a system...
of the quantum system and
 is the inverse temperature. With these notations, the Bogoliubov inner product takes the form
is the inverse temperature. With these notations, the Bogoliubov inner product takes the form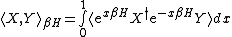
where
 denotes the thermal average with respect to the Hamiltonian
denotes the thermal average with respect to the Hamiltonian 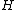 and inverse temperature
and inverse temperature 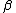 .
.In quantum statistical mechanics, the Bogoliubov inner product appears as the second order term in the expansion of the statistical sum: