Bogoliubov causality condition
Encyclopedia
Bogoliubov causality condition is a causality condition
for scattering matrix (S-matrix) in axiomatic quantum field theory
. The condition was introduced in axiomatic quantum field theory by Nikolay Bogolyubov
in 1955.
of a function
defined on the Minkowski space
. This function characterizes the intensity of the interaction in different space-time regions: the value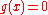 
at a point 
corresponds to the absence of interaction in 
, 
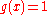corresponds to the most intense interaction, and values between 0 and 1 correspond to incomplete interaction at 
. For two points 
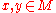, the notation 
means that 
causally precedes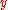 
.
Let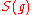
be scattering matrix as a functional of 
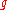. The Bogoliubov causality condition in terms of variational derivatives has the form:
Causality conditions
In the study of Lorentzian manifold spacetimes there exists a hierarchy of causality conditions which are important in proving mathematical theorems about the global structure of such manifolds. These conditions were collected during the late 1970s....
for scattering matrix (S-matrix) in axiomatic quantum field theory
Axiomatic quantum field theory
Axiomatic quantum field theory is a mathematical discipline which aims to describe quantum field theory in terms of rigorous axioms. It is strongly associated with functional analysis and operator algebras, but has also been studied in recent years from a more geometric and functorial...
. The condition was introduced in axiomatic quantum field theory by Nikolay Bogolyubov
Nikolay Bogolyubov
Nikolay Nikolaevich Bogolyubov was a Russian and Ukrainian Soviet mathematician and theoretical physicist known for a significant contribution to quantum field theory, classical and quantum statistical mechanics, and to the theory of dynamical systems; a recipient of the Dirac Prize...
in 1955.
Formulation
In axiomatic quantum theory, S-matrix is considered as a functionalFunctional
Generally, functional refers to something able to fulfill its purpose or function.*Functionalism and Functional form, movements in architectural design*Functional group, certain atomic combinations that occur in various molecules, e.g...
of a function
defined on the Minkowski spaceMinkowski space
In physics and mathematics, Minkowski space or Minkowski spacetime is the mathematical setting in which Einstein's theory of special relativity is most conveniently formulated...
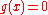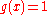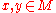. This function characterizes the intensity of the interaction in different space-time regions: the value at a point corresponds to the absence of interaction in , corresponds to the most intense interaction, and values between 0 and 1 correspond to incomplete interaction at . For two points , the notation means that causally precedes 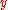.Let
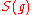be scattering matrix as a functional of 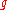. The Bogoliubov causality condition in terms of variational derivatives has the form:
