
Blanuša snarks
Encyclopedia
In the mathematical
field of graph theory
, the Blanuša snarks are two 3-regular graph
s with 18 vertices and 27 edges. They were discovered by Croatian
mathematician
Danilo Blanuša
in 1946 and are named after him. When discovered, only one snark was known—the Petersen graph
.
As snark
s, the Blanuša snarks are connected, bridgeless cubic graph
s with chromatic index equal to 4. Both of them have chromatic number 3, diameter 4 and girth 5. There are non-hamiltonian but are hypohamiltonian
.
D4, the group of symmetries of a square.
The automorphism group of the second Blanuša snark is an abelian group
of order 4 isomorphic to the Klein four-group
, the direct product
of the Cyclic group
Z/2Z with itself.
The characteristic polynomial
of the first and the second Blanuša snark are respectively :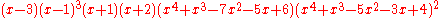
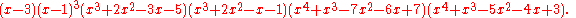
 and
and 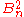 . The Blanuša snarks are the smallest members those two infinite families.
. The Blanuša snarks are the smallest members those two infinite families.
In 2007, J. Mazak proved that the circular chromatic index of the type 1 generalized Blanuša snarks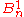 equals
equals  .
.
In 2008, M. Ghebleh proved that the circular chromatic index of the type 2 generalized Blanuša snarks equals
equals 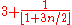 .
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
field of graph theory
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
, the Blanuša snarks are two 3-regular graph
Regular graph
In graph theory, a regular graph is a graph where each vertex has the same number of neighbors; i.e. every vertex has the same degree or valency. A regular directed graph must also satisfy the stronger condition that the indegree and outdegree of each vertex are equal to each other...
s with 18 vertices and 27 edges. They were discovered by Croatian
Croats
Croats are a South Slavic ethnic group mostly living in Croatia, Bosnia and Herzegovina and nearby countries. There are around 4 million Croats living inside Croatia and up to 4.5 million throughout the rest of the world. Responding to political, social and economic pressure, many Croats have...
mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
Danilo Blanuša
Danilo Blanuša
Danilo Blanuša was a Croatian mathematician, physicist, engineer and a professor at the University of Zagreb. He was Serb and he was born in Austro-Ugarska monarchy ....
in 1946 and are named after him. When discovered, only one snark was known—the Petersen graph
Petersen graph
In the mathematical field of graph theory, the Petersen graph is an undirected graph with 10 vertices and 15 edges. It is a small graph that serves as a useful example and counterexample for many problems in graph theory. The Petersen graph is named for Julius Petersen, who in 1898 constructed it...
.
As snark
Snark (graph theory)
In the mathematical field of graph theory, a snark is a connected, bridgeless cubic graph with chromatic index equal to 4. In other words, it is a graph in which every vertex has three neighbors, and the edges cannot be colored by only three colors without two edges of the same color meeting at a...
s, the Blanuša snarks are connected, bridgeless cubic graph
Cubic graph
In the mathematical field of graph theory, a cubic graph is a graph in which all vertices have degree three. In other words a cubic graph is a 3-regular graph. Cubic graphs are also called trivalent graphs....
s with chromatic index equal to 4. Both of them have chromatic number 3, diameter 4 and girth 5. There are non-hamiltonian but are hypohamiltonian
Hypohamiltonian graph
In the mathematical field of graph theory, a graph G is said to be hypohamiltonian if G does not itself have a Hamiltonian cycle but every graph formed by removing a single vertex from G is Hamiltonian.-History:...
.
Algebraic properties
The automorphism group of the first Blanuša snark is of order 8 and is isomorphic to the Dihedral groupDihedral group
In mathematics, a dihedral group is the group of symmetries of a regular polygon, including both rotations and reflections. Dihedral groups are among the simplest examples of finite groups, and they play an important role in group theory, geometry, and chemistry.See also: Dihedral symmetry in three...
D4, the group of symmetries of a square.
The automorphism group of the second Blanuša snark is an abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
of order 4 isomorphic to the Klein four-group
Klein four-group
In mathematics, the Klein four-group is the group Z2 × Z2, the direct product of two copies of the cyclic group of order 2...
, the direct product
Direct product of groups
In the mathematical field of group theory, the direct product is an operation that takes two groups and and constructs a new group, usually denoted...
of the Cyclic group
Cyclic group
In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
Z/2Z with itself.
The characteristic polynomial
Characteristic polynomial
In linear algebra, one associates a polynomial to every square matrix: its characteristic polynomial. This polynomial encodes several important properties of the matrix, most notably its eigenvalues, its determinant and its trace....
of the first and the second Blanuša snark are respectively :
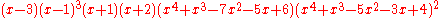
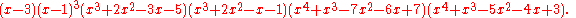
Generalized Blanuša snarks
There exists a generalisation of the first and second Blanuša snark in two infinite families of snarks of order 8n+10 denoted and
and 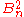 . The Blanuša snarks are the smallest members those two infinite families.
. The Blanuša snarks are the smallest members those two infinite families.In 2007, J. Mazak proved that the circular chromatic index of the type 1 generalized Blanuša snarks
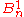 equals
equals  .
.In 2008, M. Ghebleh proved that the circular chromatic index of the type 2 generalized Blanuša snarks
 equals
equals 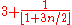 .
.

